Early Mathematics Counts: Promising Instructional Strategies From Low- and Middle-Income Countries

Introduction

Research from around the world has demonstrated that mathematical skills are essential to later academic achievement, economic well-being, and participation in democratic processes (Duncan et al., 2007; Duncan & Magnuson, 2011; Foster, 2010; Siegler et al., 2012). Multiple studies provide evidence for these claims. In a study of 23 countries, Hanushek and colleagues (2015) estimated that a one-standard-deviation increase in numeracy skills is associated with an average increase of 17.8 percent in hourly wages. When cognitive skills, represented by math and science skills in international tests, are added to a model that includes initial income and years of schooling, the variation contributing to economic growth increases from 0.25 to 0.73 (adjusted R²; Hanushek & Woessmann, 2008). Cokely et al. (2018) found that performance on conventional and statistical measures of numeracy explained 34 percent of the variance in general decision-making skills. All these findings point to the importance of supporting mathematical development across the school years and beyond.

At the same time, access to primary education has increased globally by a large margin (estimated 93 percent net enrollment in primary school in 2015; Education for All Global Monitoring Report Team, 2014; United Nations, 2015). However, this rapid pace of expansion of access to education has not resulted in the quality instruction necessary for later academic achievement and employment. Performance on student assessments indicates that many are not learning as much as they could and should, despite increased access to education. Worldwide, one-third of children who have completed primary school have not attained even basic skill levels in mathematics (Education for All Global Monitoring Report Team, 2014). This failure to ensure minimal levels of quality in many public education systems worldwide represents not only an inefficient use of public and private resources, but also a lost opportunity for individual students, societies, and economies. The problem of low student learning outcomes despite large investments in education is well known (Kremer & Holla, 2009); however, classroom-level solutions are less familiar to policy and decision makers.

A broad base of research shows that teacher effectiveness is a significant determinant of student learning. Although income, health, parent education and other factors contribute to learning outcomes, the single most important school-based factor in student learning is teacher effectiveness (Rivkin et al., 2005; Rockoff, 2004). Studies done in diverse contexts, for instance in the United States, Cambodia, and Guatemala, have shown that there is a strong link between teachers’ knowledge of how to teach mathematics and student achievement (Hill et al., 2005; Marshall et al., 2009; Marshall & Sorto, 2012). In a review of teacher effects, Nye, Konstantopoulos, and Hedges (2004) found that teacher effects on students’ academic performance explain 1 to 21 percent of the variance (p. 239), and in their own study found the greatest effects for performance in mathematics achievement. Assuming that teachers must use effective instructional strategies in order to be effective, we focus in this paper on identifying the instructional strategies found in the early years in low- and middle-income countries.

Students must learn basic math skills in early grades, as future learning depends on these foundational concepts (Duncan et al., 2007). In low- and middle-income countries, there is an expanding literature on reading instruction and learning, but much less on math instruction. Given teachers’ centrality to the learning process and the need for evidence-based guidance, in this paper we examine the research on early grade mathematics teaching strategies in low- and middle-income countries. These strategies are viewed through the lens of interventions, research-based inquiry into how changes in strategies result (or do not result) in improved academic outcomes.

The teaching of foundational mathematical skills has been a topic of substantial research over the past 30 years, though this research is largely conducted in high-income countries (D. Clements & Sarama, 2014; Drent et al., 2013; English, 2008). There has additionally been a concerted effort to identify highly effective teaching strategies in primary school mathematics in high-income countries, where education ministries and professional organizations have articulated teaching goals and principles (Australian Association of Mathematics Teachers (AAMT), 2006; National Council of Teachers of Mathematics, 2014; National Research Council et al., 2001; Parveva et al., 2011; Swan et al., 2008). Recently, broad international efforts have been made to understand how the set of skills and approaches to improving classroom learning are applicable on the global level (Learning Metrics Task Force, 2013). It is to this last category that we apply our efforts, as it is an area of great need and little existing analysis.

It is important to note that the area of interest that we review—teacher strategies within interventions targeting early grade mathematics in low- and middle-income countries—is sparse and/or not well articulated: in a recent review of robust studies that evaluated causal links between system-wide interventions and student outcomes, Fleisch et al. (2016) list only nine such studies. Many more unpublished reports exist than peer-reviewed studies. This may be because the primary purpose of these studies is to evaluate the efficacy of the interventions, and not necessarily to build a research base.

We recognize that informally published reports are not subject to the same rigorous fact checking and transparency that peer-reviewed studies are. Nevertheless, we felt it important to include these reports in our review for two reasons. First is their presence in the field. Many of the early mathematics interventions that exist are implemented by organizations that produce reports on efficacy that do not find their way into peer-reviewed journals. Excluding these interventions would ignore considerable evidence on instructional strategies. Second, we hope that our analysis will encourage authors of such reports to (1) communicate their findings more broadly and, in doing so, be held to similar standards as their peer-reviewed colleagues and (2) when possible, submit to peer-reviewed journals. We recognize that there may be a difference in reliability between informally published reports and peer-reviewed articles, and so we identify in Table 1 later in this paper those studies that are peer-reviewed.

Considering the number of interventions implemented over the past 25 years, the evidence base is relatively scarce and not well articulated. Our aim is to provide an in-depth description of instructional strategies used in interventions in low- and middle-income countries. We focus our review on interventions at the classroom level that had measurable outcomes, and therefore we exclude studies focusing on pre-service teacher education, with the recognition that pre-service support is essential to the success of any educational system.

We chose studies that had measurable outcomes because they are required in building a research base on effective strategies. However, given the studies we included, it would be impossible to tie specific instructional strategies to student learning outcomes for several reasons. First, there is no single “best” practice (Parveva et al., 2011; Swan et al., 2008). Recommended strategies are not something to follow blindly as one teaches, but rather a toolbox of approaches that teachers can select for the mathematical task at hand, taking into account the needs of the students at that moment in time. Given that all of the articles and reports we reviewed were about interventions, where the goal was to improve learning outcomes and not test a specific practice, it is not surprising that they tended to include multiple strategies as a suite of “best strategies” to improve learning. Linking learning outcomes to one specific instructional practice cannot be done reliably in these cases.

Second, the reports and articles were not focused on describing instructional strategies, but rather on reporting the results of the evaluation. We reviewed the interventions with an eye toward gathering information on the classroom instruction—for example, hands-on learning, sample lesson plans, or specific activities or games played during class. Given these glimpses into classrooms, we compiled a set of four strategies from the various studies. However, given the sparsity of the information provided and a lack of isolated strategies, we did not feel comfortable linking specific strategies to outcomes reported by the projects. In other words, while we report on the impacts of the various interventions, we do not link these impacts to isolated strategies.

Finally, we note that many factors other than classroom teaching may affect children’s acquisition of mathematical knowledge and skills. Malnutrition, access to clean drinking water, health, civil and home strife, community support for education, parental education, access to material goods, distance to school, and classroom ratios can all affect student learning. However, with heartfelt acknowledgment that solving these issues is essential in changing the lives of children in low-performing education systems around the world, this paper focuses on classroom strategies with the aim of gathering evidence to support policy responses to systemic quality failures in low- and middle-income country education systems.

Research Base on Effective Strategies in Early Mathematics Instruction

We begin with a review and summary of the available evidence base on instructional strategies in early grade mathematics, drawing on research across the globe, although a majority of the research is from high-income countries. Below are descriptive summaries of five strategies frequently cited in the literature. We reviewed several country-level documents that specify instructional practices and found confirmation for the five strategies listed below from the United Kingdom (Swan et al., 2008), Australia (Australian Association of Mathematics Teachers (AAMT), 2006), United States (National Council of Teachers of Mathematics, 2000, 2014), and Singapore (Ministry of Education, Singapore—Curriculum Planning and Development Division (MOE Singapore), 2012).

Using Multiple Representations, Including Manipulatives

In mathematics, students frequently benefit from exposure to a variety of representations when examining ideas and concepts and solving problems. Teachers who have facility with multiple representations and modeling are able to support development in a greater number of students than can teachers who can only see a concept or problem from a single perspective. Representations, at their best, allow students to “see” the mathematics in a problem.

As in many aspects of mathematics, there is a developmental progression of the use of representations (Siegler & Lortie-Forgues, 2014). In the early years, these representations are not symbolic^[1]—instead, they embody the problem in a very real way. Examples include counting real objects (e.g., children in the classroom), joining two sets of pebbles, and examining a paper triangle. As students’ mathematical abilities grow, their use of manipulatives (such as pebbles) changes from using the actual objects under question (e.g., “How many pebbles do you have?”) to using manipulatives (such as pebbles or fingers) to represent a real-world problem (e.g., “Two children are in a boat and two more children join them. Now how many children are there all together in the boat? If you want, you can use these pebbles, your fingers, or paper and pencil to help you solve the problem.” (Uttal et al., 1997) and later a purely symbolic problem (e.g., while pointing at the equation “2 + 2 = ?” the teacher asks the student, “What does two plus two equal? If you want, you can use these pebbles, your fingers, or paper and pencil to help you solve the problem.”).

Representations are used throughout mathematical problem solving. Base-ten concepts are taught in many countries with sticks or representations of sticks, gathered into or illustrated as bundles of 10. Ten frames and arrays are other common representations used in developing number sense. Fractions are frequently taught with area models (e.g., a square divided into four equal squares or a circle divided into four equal parts for continuous quantities or countable objects for discontinuous quantities) and number lines; negative numbers can be taught with thermometers, elevators, money, and number lines; and division with paper and pencil drawing and grouping. Representations are not restricted to objects that can be seen; they can also be expressed through oral or written language and gestures.

Simply using a variety of representations in the classroom to model problems does not guarantee mathematical development (Clements & Sarama, 2014, pp. 312–315). Students must be able to not only make the connection from the problem to the representation but also understand multiple aspects of the representation. An example is the use of area models in the teaching of fractions. Many students understand that a circle divided into three parts can represent thirds. However, those same students may not understand a fundamental rule of fractions—that the parts must be equal—especially if they always see a circle divided evenly. Researchers have discussed the use of non-routine representations as a tool for drawing out students’ understandings and misconceptions (Gearhart et al., 2015).

Using Developmental Progressions

Many studies that examine teacher strategies include an emphasis on knowledge of developmental progressions (Ma, 1999; Platas, 2014; Vernaud, 1992). Several bodies of research have continued to refine their models and test validity and reliability around this topic and have shown experimentally that such knowledge contributes to mathematics achievement (Carpenter et al., 1989; D. H. Clements & Sarama, 2008; Hill et al., 2005; Starkey et al., 2005).

Over the years, several researchers have conducted studies that suggest that the best way to support mathematical development is to build on a solid foundation of student knowledge in a developmentally appropriate way. Much of this work shows progressions within subdomains; students generally progress from smaller set sizes and less sophisticated problems to larger sets and more sophisticated problems within those subdomains. However, it is important to keep in mind that experience plays a large part in students’ acquisition of mathematical knowledge. As an example, students who have extensive experience in fair-sharing through informal math experiences (i.e., sharing toys or food) may be able to grasp simple division word problems before they grasp subtraction word problems. Therefore, instruction should not be based on a lockstep scope and sequence, but instead flexibly based on individual student knowledge. This flexibility is termed differentiated instruction.

Importantly, conceptual understanding and computational fluency are both central in the support of related developmental progressions (Baroody, 2012). Considerable research on arithmetic development shows that children initially rely on procedural strategies, but then gradually use memory retrieval (Ashcraft, 1982) and that the ability to solve more complex arithmetic problems is positively influenced by arithmetic fluency (Geary, 2000). Gersten and colleagues (2009), in a review of studies with students who struggle with mathematics, concluded that “general mathematics proficiency will improve when fact fluency improves” (p. 79) and recommend that instruction include an emphasis on relationships between facts (e.g., 2 + 3 = 5; 5 – 2 = 3), use of materials (worksheets, number lines, and arrays of blocks), explicit teaching of strategies for building fact fluency (such as counting on from a given number), and devoting 10 minutes per session on activities that promote fact fluency.

Supporting Student Explanation and Justification

In the past, classroom discourse or conversations around and within the topic of mathematics (sometimes referred to as math talk) did not garner much space in the research literature on early mathematical development. However, recent research has illustrated the importance of this activity as early as preschool (Klibanoff et al., 2006; Parrish, 2010). Mathematical discourse in primary and secondary school has long been considered an important aspect of mathematics teaching and learning (Nickson, 1992). During the 21st century, our understanding of teaching has changed from a transmission view (teacher to student) to one of participation (interactions between teachers and students). This participation requires students to explain their thinking and justify their solutions. Lampert and Cobb (2003), writing on the research support for mathematical communication, cite studies that correlate high mathematical achievement with student behaviors of giving elaborate explanations to peers and teacher behaviors of higher-level questioning. Lampert and Cobb also examined the learning opportunities that can arise through discourse. These include (a) mathematizing (considering concrete activities in mathematical terms), (b) negotiated defining and genre instruction (the intersection of defining mathematical terms that make sense to students and academic speech, what Ball (1993b) describes as the dilemma of teaching mathematical word meanings), (c) participation structure for doing and learning mathematics (this can include explanation and justification), and (d) conceptual discourse and big mathematical ideas (Lampert & Cobb, 2003, p. 240–244). Ball and others also consider students’ misconceptions to be a primary source of valuable classroom discussion (Ball, 1993b; Webb et al., 2014).

Much of the research evidence on effective teaching strategies includes some form of support for student explanation and justification. While group work in classrooms can consist of a variety of activities (including worksheet-based seat work), research-based effective strategies are distinctively interactive and include asking students to help one another understand mathematics concepts or procedures (Agodini et al., 2010), explain their thinking (Fennema et al., 1989), verbalize thought processes (Gersten et al., 2009), describe their thinking and solution strategies (National Research Council et al., 2001), participate in class discussions and peer problem-posing (Saxe et al., 2001), and answering teacher-posed questions (Sloan, 1993).

However, supporting students’ explanation and justification in real time is not easy to do. Clarke (2003) explored teacher attitudes and strategies in light of a reform being enacted in India, the District Primary Education Project, which emphasized child-centered, active learning, including facets of explanation and justification. Clarke found that although surface features of the reform were put into place in classrooms, at its core, observed instructional strategies remained focused on rote and repetitive traditional instruction, aligning closely with teachers’ self-reported attitudes. This study suggests that although efforts focusing on student explanation and justification have promise, attempts to change teacher strategies need to be linked to changes in teacher knowledge and attitude (Fullan, 1993).

In Kenya, Hardman and colleagues (2009) examined several facets of teacher interactions, including giving praise in feedback, encouraging student answers and questions, commenting on student answers by rephrasing or elaborating on an answer, and using open-ended questions. While child effects were not studied, teachers in the treatment group used more of these techniques at the end of the intervention than did teachers in the control group.

Integrating Formal and Informal Mathematics

There is ample documentation from diverse settings such as the United States, Brazil, India, Mexico, Benin, and elsewhere that children engage in informal mathematical activities as a part of their everyday lives (Bodovski & Farkas, 2007; B. Clarke et al., 2006; Davis & Ginsburg, 1993; Guberman, 1999; Khan, 1999; Saxe, 1991; Sitabkhan, 2009, 2015; Taylor, 2013). They play games in which numbers are used. They count objects. They buy things from stores, familiarizing themselves with denominations of currency, adding up total costs, and calculating change. As children explore their physical world, they encounter geometrical shapes, which they manipulate through play. In all these ways and more, children are actively learning and adapting mathematical concepts to solve problems in their daily lives.

In addition to recognizing and validating students’ informal mathematical knowledge in the classroom, there is a role for explicit instruction that aims to bridge and connect informal with formal mathematics. Instruction that aims to connect the two types of knowledge can support deeper understanding of mathematics, as informal mathematics concepts give meaning to abstract concepts.

A project in Papua New Guinea called the Curriculum Reform Implementation Project developed syllabi for instruction at the local level and integrated locally developed materials in classrooms. In addition to promoting a shift to more student-centered teaching, the project developed materials related to cultural mathematics, which aimed to integrate traditional knowledge of mathematics into the school, such as using local items to support counting and operations. A study found that the cultural mathematics syllabi did not become integrated into the classroom mathematics lessons as intended, and most teachers reported not making connections between traditional and formal mathematics (T. Evans et al., 2007). Although this research points to the importance of integrating and building on informal mathematics for increasing student learning outcomes, it also points to the difficulty in being able to do it well, especially in terms of fostering new strategies with teachers. Research is needed on ways to integrate informal knowledge in the classroom through teacher support, and there is evidence that teacher uptake of new strategies requires effective teacher training programs (Bruns & Luque, 2015; Yoon et al., 2007).

Making Connections Between Mathematical Domains and Concepts

Ma emphasizes aspects of “profound understanding of fundamental mathematics,” which include basic ideas, connectedness, multiple representation, and longitudinal coherence (1999, p. xxv). Other researchers over the years have emphasized the importance of the connections attribute of mathematical understanding (Ball, 1993a; Fennema et al., 1989) in teacher education and practice. Evidence from research in low-income countries indicates that this connectedness is important in low-income countries as well. Several studies support the importance of connections in mathematics in their curriculum design (DeStefano et al., 2013; Fauzan, 2002).

What is meant by connections? Even though mathematics is frequently divided into subdomains such as geometry and operations, mathematics as a field is full of connections. As an example, geometry and operations have many connections: perimeter and area can be calculated using multiplication, and area representations such as divided rectangles can be useful for teaching multiplication. Growing patterns using shapes (triangle, triangle, star, star, star, star, circle, circle, circle, circle, circle, circle…) can be translated to a growing pattern using numbers (2, 4, 6, …). Algebra depends on the ability of students to understand properties of operations: addition, subtraction, multiplication, and division.

Methodology

Identification of Studies

To identify relevant evidence to review instructional strategies in early mathematics from low- and middle-income countries, we conducted a search to access a broad base of scholarship, including non-journal-based research. We used Google Scholar and EBSCO. The search terms included classroom, developing countries, early grade mathematics, early math, elementary, mathematics, maths, pedagogy, practice, primary, results, and teacher strategies. Using several combinations of search terms, we searched for papers published between 1993 and 2018. Even with these broad-based search engines, we felt that some valuable reports would be missed.

We therefore examined bibliographies for possible references of interest (including the latest Education for All Global Monitoring Report Team, 2014) and queried multiple researchers and practitioners in the field to gather reports that may inform our analysis but had not yet been published or were not intended to be manuscripts. Our criteria for inclusion consisted of the following:

1. Classroom-level interventions that included a math component, with or without teacher training components, in low- and middle-income countries

2. Focus on preschool to grade 3 mathematics

3. Measurable learning outcomes

4. Availability of the article/report

All included studies had to explicitly address aspects of instructional strategies of the intervention, not just general early grade mathematics research.

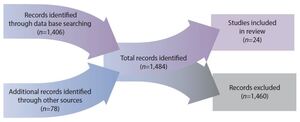
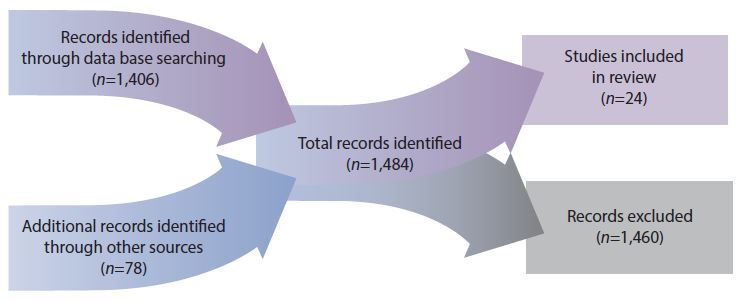
To narrow the range of studies, we only included articles and reports that contained classroom-level interventions. Twenty-four studies met these criteria. While this analysis is not all-inclusive of research performed during the designated time span, we exerted considerable effort to access pertinent studies. Figure 1 illustrates our search process.

Figure 1.Search process

Identification of Instructional Strategies

Once we identified the 24 studies, we used an iterative process to identify instructional strategies, and then coded the studies for these strategies. We began with the development of the descriptive summaries identified above, where we reviewed available literature to better understand the types of instructional strategies used in early mathematics classrooms, and the evidence behind these strategies. As shown in the previous section, we were able to group the evidence into five strategies.

We then reviewed the studies we had identified through our search with these five strategies in mind, but also with an eye toward identifying any other strategies that were used that may not have been captured in the previous summaries. We conducted these reviews separately and then discussed them in detail. After the review, we determined that for four of the five strategies (multiple representations, developmental progressions, explanation and justification, and informal and formal mathematics), we were able to see substantial evidence in the chosen studies. For the fifth strategy, connections between domains and concepts, we were not able to identify any evidence in the studies, so we decided not to include this strategy. We did not find substantial evidence for any additional strategies.

Our rationale for organizing our search as described above was based on the assumption that mathematics is not context- or culture-neutral (Nasir et al., 2008) and that any instructional practice that is used in one context will manifest itself differently in another context. Therefore, although we did begin with the available literature base, we reviewed the identified studies with an eye toward better understanding whether these strategies were being used, and if so, what they looked like in their particular context. To this end, we created a codebook of the different strategies (descriptors) which would constitute evidence for each one, as described in the following list:

• Using multiple representations, including manipulatives: instruction that

  • addresses knowledge at both concrete and abstract levels

  • uses concrete objects, including locally made objects

  • provides exposure to a variety of representations when examining ideas and concepts and when solving problems

• Knowing and using developmental progressions: instruction that

  • is sequenced

  • builds on prior knowledge

  • is differentiated

  • provides appropriately challenging tasks

  • uses both conceptual and procedural knowledge to build fluency

• Supporting student explanation and justification: instruction that

  • draws on student thinking as a resource for explanation and justification

  • encourages students to justify their solutions

  • asks questions such as “why” and “how”

• Integrating formal and informal mathematics: instruction that

  • recognizes and validates students’ informal thinking

  • integrates knowledge students bring from home and other out-of-school contexts

We double-coded each of the 24 studies using the criteria above. If we found evidence that a practice aligned with codebook descriptors, we coded it as using that instructional practice. Where we disagreed over coding, we discussed the evidence and came to a mutual agreement on the coding category.

In the remaining sections of this paper, we discuss the evidence of these four strategies in the chosen studies in depth.

Results

Table 1 provides summary information of the 24 studies that met our criteria for inclusion. The table contains the authors and year of the study, the research design, the number of treatment participants, the country of focus, and the included strategies. It should be noted that we were limited to the information reported in the studies. Many of the studies did not adequately describe instructional strategies. Most studies focused on student learning outcomes as a result of one or more instructional strategies but did not include important information such as dosage or how these strategies were integrated with one another. When multiple sources for a study were available, we used information from both the more informational unpublished reports as well as the peer-reviewed publications that followed. In the rest of this section, we discuss the supporting evidence from the 24 studies.

Using Multiple Representations, Including Manipulatives

Sixteen of the 24 studies included evidence on effective use of representations, which was the most commonly mentioned practice across the 24 studies. A majority of these studies focused on the use of concrete manipulatives to support active learning and math games but did not explicitly mention using multiple representations and models. There was often limited information provided about how concrete manipulatives were used.

The Numeracy Boost interventions in Malawi and Bangladesh provided support through mathematics learning in both in-school and out-of-school environments (Guajardo et al., 2013; Jonason et al., 2014). Teachers were trained in mathematics content and provided with kits that included games and manipulatives for learning. Families were also provided with support for mathematical development in the home, and community-based math camps were developed and convened. The two studies employed randomized controlled trial (RCT) designs to test the efficacy of the intervention. In Bangladesh, the authors found that grade 2 children who received both Numeracy Boost and its reading counterpart, Literacy Boost, showed significant increases in most numeracy skills, including skip counting by 5’s, missing number recognition, subtraction, and word problems (Jonason et al., 2014). In Malawi, the Numeracy Boost intervention did not increase student math scores (Guajardo et al., 2013).

In Paraguay, preschool students were taught with translated versions of the Big Math for Little Kids curriculum (Greenes et al., 2004; Näslund-Hadley et al., 2014). Many activities included manipulatives, and the studies provided some information on how they were used. For example, activities included organizing balls and sticks into groups. Students in the treatment group made significant gains over the business-as-usual control group in a mathematics test (a 0.16 standard deviation over just five months; Naslund-Hadley et al., 2012; Naslund-Hadley, Parker, & Hernandez-Agramonte, 2014).

In studies focusing on 5- to 6-year-old children in Ethiopia, Rwanda, and Mozambique, Save the Children’s Emergent Literacy and Math Intervention showed impressive gains (Amente et al., 2013; Martinez et al., 2013; Save the Children, 2015). The program focused on games and play-based activities with manipulatives. In Ethiopia, 5- to 6-year-old children in the treatment group showed gains of 49 percent in a mathematics assessment over a 5-month implementation period (Amente et al., 2013). Two comparison groups, students enrolled in similar early childhood centers without the intervention and students not enrolled in preschool, made gains of 13.9 and 1.9 percent, respectively. Gains were particularly strong in shape and number identification. In Rwanda, a similar intervention followed children from preschool to grade 1. Although results showed strong gains in math in the treatment group as compared with the control group, these findings were more pronounced from baseline to midline, versus midline to endline, when children were in grade 1. The authors conclude that the gains made during preschool did not last into grade 1. Explanations for similar results in other studies include repetition of curricula in grades following preschool, producing fadeout in learning (Engel et al., 2013; Watts et al., 2017).

Martinez and colleagues conducted an external evaluation of the Emergent Literacy and Math Intervention in Mozambique. Using an RCT design, children in the preschool treatment group were exposed to a 25-minute math circle activity that used the contents of math bags that were provided to the children. These bags held manipulatives such as string, sticks, shells, seeds, and bottle caps. Classroom activities that made use of these manipulatives included counting, sorting, comparing, and addition/subtraction. When compared with children in the control group (95 percent of whom had not enrolled in a preschool), teachers reported that children in the treatment group, on average, had more interest in mathematics games and showed a greater ability to sort and classify objects, achieve one-to-one correspondence, count to 20, recognize geometric shapes, and state the larger of two numbers (Martinez et al., 2013).

In another research study on preschool curricula, Hembold (2014) compared student-learning outcomes in classrooms that used an adult-directed play-based curriculum versus classrooms that used a worksheet-based curriculum. The adult-directed play-based curriculum was administered by teachers in seven different classroom settings over 30 weeks in rural, urban, and township areas in South Africa. The curricula focused on teacher-led activities and games, with a special emphasis on the use of manipulatives. Students spent approximately 30 minutes in small group activities and 40 minutes in large group activities. Under quasi-experimental conditions, students in the adult-directed play-based group scored significantly higher on a mathematical aptitude assessment. Qualitative data from the study showed that teachers enjoyed the program and intended on sustaining it after the study (Hembold, 2014). Although this study was embarked upon to meet the requirements for a master’s degree, the rigor with which it was implemented was quite remarkable.

The Tayari intervention in Kenya was unique in that attention was paid to how best to facilitate the use of manipulatives and other representations within a lesson (Piper et al., 2018). The authors describe how lessons were created to minimize the diversity of materials needed in order to ease the burden on the teacher of providing or creating multiple materials. Results from students (4–6 years old) who received 2 years of the intervention showed a statistically significant increase of 0.31 SD in performance on the numeracy index.

Opel and colleagues conducted two intervention studies in Bangladesh with preschool children (Opel et al., 2006, 2012). The 2006 intervention, supported by Education Development Resource Center and BRAC University, relied on active learning methodologies including games with different manipulatives that were locally sourced. Children’s math scores for schools in the treatment group (n = 5) increased slightly from pre- to post-test as compared with the control group after only 6 weeks of the intervention (Opel et al., 2006). Encouraged by these results, Opel and colleagues developed a 9-month intervention that was more comprehensive. The 2012 intervention, in addition to the active learning methodologies, included activities adapted from Little Math for Big Kids (described earlier; Greenes, Ginsburg, & Balfanz, 2004). Children’s math scores in schools in the treatment group (n = 9) almost doubled from pre- to post-test; the children in the control group did not perform as well (Opel et al., 2012). We commend the authors of both Opel et al. studies for the thorough way in which they described the details of the interventions.

The PRIMR project was a reading and mathematics intervention project that included teacher guides, student activity books, and teacher support through trainings and monthly coaching visits. The PRIMR project emphasized in their teacher training that grades 1 and 2 students need to be able to touch and feel mathematics objects to develop a deep understanding of mathematics (Piper et al., 2016; Piper & Mugenda, 2014). Contrary to traditional instructional strategies in Kenya (e.g., call and response, blackboard writing and copying), the PRIMR curriculum used manipulatives and hands-on activities in its implementation. The project used an RCT to test the efficacy of the intervention. Compared with the control group, students in grade 1 made statistically significant greater gains on the Early Grades Mathematics Assessment (EGMA) on a composite score made up of the number identification and one-digit addition and subtraction tasks. Students in grade 2 made statistically significantly greater gains on a composite score made up of number comparison, missing number, two-digit addition and subtraction, and word problems tasks.

Bekman et al. (2011) measured the success of a 10-week literacy and numeracy summer intervention for disadvantaged 6-year-old students in Turkey. The intervention included the use of objects and pictures to support basic mathematical skills, such as addition and subtraction. Using pre-post measures, students in the treatment group scored significantly higher on post-assessment numeracy measures. The authors conclude that despite the short duration of the intervention, the intensive support for disadvantaged students showed promise.

The use of manipulatives is the most frequently observed use of representations in our analysis and is featured widely in the literature, often described as “hands-on learning” (Brombacher, 2015; Gallego et al., 2017; McEwan, 1998; Vaijayanti et al., 2016). We did not find any evidence of studies using multiple representations such as number lines or area models for instruction. Given the limited information provided, it is unclear whether these multiple representations were truly not included in the intervention or were excluded only in descriptions of the intervention.

Knowing and Using Developmental Progressions

In our analysis of evidence from the 24 selected studies, we found that successful interventions frequently provide teachers with support in gaining an understanding of developmental progressions. In all, 10 of the 24 studies mentioned developmental progressions and sequencing as part of their intervention.

In Liberia, an intervention with an RCT design (King et al., 2015) resulted in raised student outcomes in some early numeracy skills, although they decreased in other skills. Grades 2–3 teachers were given sequenced guides as well as instructional materials for grade 1 to provide support for those students who were not performing at their grade level. Learning outcomes were measured using the EGMA, and results show that children’s outcomes decreased between midline and endline in some numeracy skills. However, the Ebola outbreak in Liberia severely disrupted the intervention, and students did not attend school for several months.

The Tayari early childhood intervention resulting in numeracy gains in Kenya, described above (Piper et al., 2018) developed sequenced lessons based on developmental progressions. Lessons repeated similar activities with increasing difficulty throughout the year. The article includes a weeks’ worth of daily lesson plans, illustrating the developmental progressions clearly.

In Jordan, an intervention that was designed to build grade 1–3 students’ foundational mathematical knowledge led to an increase in student learning gains in early mathematics tasks (Brombacher, 2015; Brombacher et al., 2015). Students in 45 schools received the intervention, which consisted of 15-minute daily routines focused on counting, manipulating numbers, and solving problems. These routines were specifically sequenced to capture developmental progressions in students’ learning of numbers by providing activities that varied in complexity and content according to student needs. Endline results showed that student performance on all EGMA subtasks except number identification increased significantly as compared with a control group.

In Paraguay’s Ministry of Education and Culture and the Inter-American Development Bank’s cultural adaptation of Big Math for Little Kids (Presser et al., 2015), they used activities and stories that developed preschool children’s ideas about number, shape, pattern, logical reasoning, measurement, operations on numbers, and space. The activities introduced the mathematical ideas in a coherent, carefully sequenced fashion, relying on developmental trajectories to inform the sequencing. Results included a narrowing of the gap between low- and high-achieving students (Näslund-Hadley et al., 2012, 2014).

In a study from India, Banerjee and colleagues (2007) found that remedial education that focused on basic skills with grades 3 and 4 students resulted in increased test scores in mathematics. One of the core elements of this study was to understand students’ prior knowledge and target instruction that would most benefit them, instead of assuming that they were on grade level. Providing this additional instruction on basic skills to only those students who need it is an example of differentiated instruction, which allows the classroom teacher to work with more advanced students.

Similarly, Gallego et al. (2017) reported on the results of a study in Peru titled Mimate where the focus was on providing instruction tailored to the level of the child three times a week. Teachers were provided with quick ways to assess students in preschool and then direct them to an appropriate activity depending on their needs. This targeted instruction relies on an understanding of progressions of learning to asses which activity a child has mastered, and which activity comes next. Results showed improvement in mathematics outcomes for the treatment group as compared with the control group after one year of intervention. However, there was a fadeout effect when learning was measured after students were in grade 1, with no statistically significant effects.

Another study from India, the Akshara Ganitha intervention (Vaijayanti et al., 2016), used an approach that drew on developmental progressions to move students in grades 1–5 through the stages of concept learning, beginning with the concrete, then representational, and then abstract. Teachers were provided with a teacher manual, mathematics kits with manipulatives, training, and in-classroom support through a field coordinator. The intervention found that students in the treatment group improved from pre- to post-test, and teacher abilities in facilitating also improved as a result of the intervention.

Fleisch and colleagues (2016) report on the Guateng Primary Language and Math Study, which was a system-wide reform program in the Gauteng Province of South Africa targeted to students in grades 1–7. For grades 1–3, the program provided learner books and scripted lessons where activities were provided that were sequenced and paced according to recent research on mathematics education. The evaluation found that numeracy scores significantly increased for students in the treatment group.

The use of developmental progressions was the second most frequently observed practice. Together, these studies suggest that knowledge of developmental progressions is an essential element of interventions in early mathematics.

Supporting Student Explanation and Justification

Six of 24 of the studies listed supported explanation and justification. In a quasi-experimental study in Zambia, researchers compared grade 2 teachers in an intervention group who had two weeks of professional development in supporting classroom discussion around problem-solving strategies to business-as-usual classrooms (Tabakamulamu, 2010). The author found that students in the intervention classroom scored significantly higher on a numeracy test delivered post-intervention.

The PRIMR study in Kenya, described earlier, supported teacher explanation through the use of a teacher’s guide, which encouraged teachers to ask students to explain their thinking on various activities (Piper et al., 2016). The Tayari early childhood program in Kenya, described earlier, embedded opportunities to build conceptual understanding by asking students questions that extended their thinking (Piper et al., 2018). For example, in a lesson on measurement, the teacher asks students to share what objects they think they should use to measure the space between two objects; instead of telling them, the teacher began a discussion about which object would be most appropriate.

Opel and colleagues (Opel et al., 2012) described various activities that were part of a preschool intervention in Bangladesh where teachers asked students to explain how they solved a problem. Students in the treatment group significantly increased their math scores from pre- to post-test as compared with a control group.

In Kosovo (Vula et al., 2017), an intervention targeted 3rd and 5th grade students’ problem-solving ability. Students were given meta-cognitive strategies (e.g., strategies to develop an awareness of their own problem solving process) and worked in small groups to collaboratively solve problems. Students in the treatment group for grade 3 did not show statistically significant improvements as compared with the control group, but there were improvements in the grade 5 treatment group. The authors suggest that 5th grade students may have had more experience with word problems, and the 3rd grade students needed more exposure.

An intervention in Rwanda focused on early mathematics, reading, and writing (Education Development Center, 2017). As part of the mathematics intervention, children were encouraged to think about numbers and flexibly manipulate them. For example, the intervention regularly used “headline stories” where children were presented with a scenario involving numbers. Instead of then asking a typical question such as, “How many all together?” the teacher asked, “What do you think of this scenario?” and encouraged children to discuss and explain their ways of thinking about numbers. Results showed significant increases in learning gains in primary 1, but not in primary 2–4.

Integrating Formal and Informal Mathematics

Five of the 24 studies capitalized on out-of-school knowledge through explicit and planned instruction, or aimed to strengthen children’s informal mathematical knowledge. Four of the five studies showed significant gains in student learning. The Tikichuela program in Paraguay (described earlier) used an adapted version of the Big Math for Little Kids curriculum that aims to connect students’ informal and formal mathematics through instruction in preschool (Näslund-Hadley et al., 2012, 2014). This program has at its core a goal to connect mathematics to everyday experiences through instruction (Greenes et al., 2004). From this study, baseline and endline results for student achievement demonstrated a 0.16 SD increase in treatment group scores when compared with the control group.

Two evaluation studies on the Escuela Nueva movement in Guatemala (de Baessa, Y & Chesterfield, 1996) and Colombia (McEwan, 1998) provide more evidence that connecting formal and informal math can be powerful in instruction. The Escuela Nueva movement involves making connections to everyday mathematical ideas and contexts to support learning of abstract concepts. In addition, the methodology strives to teach children more democratic and egalitarian modes of communication through the use of realistic mathematical scenarios. McEwan found that students in the Escuela Nueva treatment schools in Colombia showed a greater increase in performance on a mathematics exam in grade 3 than did students in a traditional school. However, this difference did not persist into grade 5. De Baessa and Chesterfield (1996) found that, although there were no significant learning gains found in mathematics achievement between treatment and control schools in Guatemala, there were favorable differences on behavioral measures, such as increased levels of student participation and more egalitarian behaviors on the part of children.

The Akshara Ganitha intervention in India (Vaijayanti et al., 2016), detailed above, encouraged children in grades 1-5 to apply their learning to real-life situations. The program used word problems as well as activities where children searched for patterns in real life and made estimations to solve problems. These strategies helped link children’s informal and formal learning in mathematics. The program also resulted in improvements both in the treatment group from pre- to post-test and in teacher facilitating abilities.

Also in India, Dillon et al. (2017) developed a game-based intervention for preschool-aged children. The aim of the intervention was to strengthen children’s intuitive, or informal, mathematics before entry into primary school with cost-effective, easy-to-play games. The results show that the intervention was successful in improving children’s informal mathematics. However, this gain in informal mathematics did not lead to improvement in formal school mathematics. It may be that that while improving informal mathematics is important, in and of itself it is not enough without strong connections being drawn between informal and formal mathematics in primary school.

Conclusions and Recommendations for Future Research

A recent meta-analysis of six systematic reviews of interventions that improve learning outcomes in low- and middle-income countries, found consistent support for pedagogic interventions that tailor teaching to student skills and that support long-term, intervention-targeted teacher training (D. K. Evans & Popova, 2015). What did we find when we examined specifically math-related interventions? We found evidence for four core strategies used in interventions in low- and middle-income contexts. These strategies dovetail with the evidence base we have on children’s mathematical development, although, as pointed out before, they are often implemented differently. The practice most commonly seen, in 16 of the interventions, was the use of manipulatives, classified under the category “multiple representations” (see Table 1). In part, the practice is prevalent because many studies mentioned “hands-on learning” using locally sourced materials. Integrating manipulatives is essential for the success of many programs; however, frequently left unsaid in the intervention descriptions is what instructional methods were used to support children’s learning while using the materials. While vague, all the studies made clear that they did not just provide materials, but also trained teachers and provided lessons. Future studies should detail how teacher instruction supported the use of manipulatives in the classroom.

In addition, missing from the discussion on most papers was how these manipulatives were used (by the teacher, by the student), and/or whether they were provided to classrooms as part of the intervention, and if so, in what quantities. We did not find evidence for the use of multiple representations such as number lines, area models, or ten frames, which could be in part due to the limited amount of information that was provided about the instruction in the studies. We hope that future studies will include these details to provide us with a better understanding of how, if at all, representations besides manipulatives are being used.

The second most frequently identified practice was the use of developmental progressions. Most of the evidence for developmental progressions came from sample materials provided and from references to sequenced content and differentiated instruction.

The strategies “connecting formal and informal mathematics” and “supporting explanation and justification” were not often seen in the 24 projects. Partly, this may be because not enough information was provided in the studies we reviewed to understand whether these strategies were included. In addition, these two strategies are among the most difficult to implement, as they require significant changes to teacher behavior.

The 24 studies and supplemental literature that we identified for this review provide descriptions of strategies in effective mathematics interventions in education systems worldwide and can inform future interventions that aim to increase student learning outcomes in early mathematics. Importantly, these descriptions provide us with insight into how strategies documented in the research literature manifest themselves in low- and middle-income countries. In addition, they raise questions about the types of research that are needed to understand nuances of how these instructional strategies are being adapted and enacted at the classroom level.

Overall, we found many studies were lacking in adequate descriptions of instructional strategies. The focus of most reports and journal articles was on reporting results of an evaluation, thus most spent time describing assessments and results of the assessments. We hope this paper prompts authors to capture and report on the strategies used in the classroom in the future.

This review has brought to light the need for more rigorous interventions in low- and middle-income countries accompanied by detailed reporting of the types of instructional strategies implemented. Although all the studies in our review had measurable outcomes (as a criterion for inclusion), we do not feel comfortable tying these outcomes to specific instructional strategies. The interventions mentioned in this paper are “packages” of strategies and procedures, so attributing any outcomes to a specific instructional practice would be inaccurate. In view of these constraints and opportunities, we list below our recommendations for research needed that will add to a comprehensive research agenda on early grade mathematics in low- and middle-income countries.

Provide Detailed Information on Instructional Strategies

Studies are needed that focus on specific instructional strategies. Currently, much research focuses on intervention studies that include mathematics instructional strategies as one of several features of an intervention (“packages,” as mentioned just above). These packages might include literacy support, teacher training or coaching, or even nutrition and health interventions. Many of these studies and reports detail the effect of the intervention by examining student learning outcomes, but very little or no space is dedicated to describing the mathematics instructional strategies used.

Most studies use multiple instructional strategies. A comprehensive approach is understandable and certainly desirable for boosting student learning outcomes. However, small studies or pilots can be integrated into larger-scale studies that isolate or manipulate the dosage of specific mathematics instructional strategies. Examining individual classroom teacher performance on use of these strategies in relation to their students’ performance would be beneficial in teasing out effects of specific teaching attributes.

Apply and Broaden Methodology Appropriately

Studies we reviewed used different methods; our evidence-based studies included RCTs and quasi-experimental studies. Future research should include varied methods in a systematic manner. Qualitative and mixed-method studies can initially focus on exploring productive strategies and quantitative studies can then focus on evaluating the effectiveness of these strategies, with qualitative inputs as to the exact elements of the strategies that worked, and how they worked, in the classroom. Studies should be linked to student learning outcomes whenever possible. However, it is also important to note that learning outcomes is only one measure of effectiveness of a program. Other measures of effectiveness, such as changes in teacher strategies, and teacher attitudes, are precursors in the process that lead to learning outcomes and are thus essential to consider.

In addition, there is a need for studies to investigate differences in learning longitudinally, as some of the studies included did (Gallego et al., 2017; Piper et al., 2018). The instructional strategies identified in this paper do not always cause immediate and measurable impact. Instead, processes of change may be slower and not immediately apparent or may be reversed over time. Longitudinal studies that follow cohorts of students or cohorts of teachers for multiple years can enhance our understanding of instructional strategies and their relationship to student learning.

Consider Additional Factors in Design

Researchers should consider various issues when designing and measuring new intervention projects. First, the local context should be at the forefront of the design of a new project. The teaching and learning of mathematics is not culturally neutral. The role of informal mathematics in early learning is crucial, and informal mathematics can vary by culture. To further the field and expand our understanding at the intersection of context, mathematics, and teaching, reports of these interventions must continue to make it into the public domain. We cannot assume that, just because an intervention worked among one population, it can be imported with equal success into another population. Even within one cultural group, not all children are the same.

Second, interventions and future studies should attempt to target underprivileged populations, such as girls, out-of-school children, and children from low socioeconomic groups, to understand what strategies or combinations of strategies may work differently with these populations. In addition, although we know quite a bit about literacy acquisition for children who come to school speaking a non-instruction language, we know very little about supporting mathematics instruction for these students.

Improve Transparency and Dissemination

Currently, many interventions are not transparent with regard to their methods and descriptions of strategies. Notable transparent standouts include the articles/reports by following authors and their colleagues: Dillon et al. (2017), Opel et al. (2006), Opel et al. (2012), Piper et al. (2018), Vaijayanti et al. (2016), and Vula et al. (2017). Opel and colleagues (2012) provided detailed information about the intervention, including an overall summary of the classroom intervention, the domains of mathematics that were covered, and sample activities for each domain. Piper and colleagues discussed how the materials were developed and provided sample pages from the teacher guide and student book. These studies allow the reader to understand the instructional strategies that were used during the intervention. Vaijayanti and colleagues explained the theoretical base of the intervention in detail and provided very clear examples of how these theoretical ideas were operationalized in their materials and teacher training. If we are to learn which strategies work best in low- and middle-income contexts, reports and articles must describe the instructional part of the intervention in greater detail.

Future studies should provide detailed descriptions of instructional strategies, teacher training, supplementary materials, intervention costs, sample sizes, and how the sample was drawn. Reports and publications should provide detailed information on instruments that measure student learning, teacher beliefs and knowledge, and instructional practice, including development, piloting, validity, and reliability so that other researchers can make use of this knowledge. Many of the studies we found do not provide detailed and transparent information.

Examine and Make Teacher Support Explicit

Many of the studies that we have reviewed point to the importance of teacher training and support, whether through pre-service or in-service programs. Researchers should examine professional development strategies that boost student learning outcomes and that have long-term effects on teacher strategies. More research is needed on how to support teachers to gain fluency in using multiple instructional approaches to maximize student understanding across learning types and ability levels. For example, integrating informal mathematical knowledge is a powerful tool if done correctly, but like many of the recommended strategies, it is challenging to do well. However, this does not mean it should be discarded; rather, innovative means can be explored and tested to understand how best to support teachers in bridging informal and formal mathematics.

The field of early grade mathematics has recently gained momentum. To sustain this momentum, practitioners, researchers, and donors need to collaborate to continue to define and enact this comprehensive research agenda.

Acknowledgments

We are grateful to the World Bank for commissioning a report that eventually turned into this paper. In particular, we are thankful to Noah Yarrow at the World Bank for his key role in promoting early mathematics work. We appreciate all the authors of the works that we have reviewed, and all the early mathematics experts in diverse countries who have contributed to our shared understanding of mathematics instruction in the early years.