A Hydro-Economic Methodology for the Food-Energy-Water Nexus: Valuation and Optimization of Water Resources

Introduction

Global supplies of fresh water are increasingly under stress from the combined effects of growing populations, rising incomes, rapid urbanization, and climate change (Mekonnen & Hoekstra, 2016; Zhao et al., 2019). Demographic and economic trends are generating ever-increasing demands for water around the world, while climate change is altering rainfall patterns and the global water cycle in ways that are still not fully understood.

Traditionally, water resources have been viewed mostly as a human right, and government policies (at the local, state, and national levels) are often designed to deliver water to households and other end-users at the lowest possible cost. Although water is needed for human survival, it is a scarce resource that must be conserved and used as efficiently as possible. In many cases, prices for water are subsidized, resulting in the end user paying less than supply and distribution costs (Convery, 2013). Such policies have led to inefficiencies in both how water is consumed overall and how it is allocated across different water using sectors (Grafton et al., 2020). Further, government policies targeting the agricultural or energy sectors—for example, subsidized energy for agricultural production that is used to pump groundwater for irrigation—can also exacerbate water allocation concerns (Scott & Shah, 2004). Inefficient consumption and allocation put undue strain on scarce freshwater supplies in many regions of the world and raise several important equity concerns, both within and across generations. These tensions over water allocation are particularly evident in arid regions with rapid population growth, ranging from the Colorado River Basin in the United States to the Jordan River Basin in the Middle East.

To encourage more-efficient water use from a local to a global scale, it is important to understand and communicate the value of water in its different uses. For example, knowledge of where and when water withdrawals will provide the most value to producers and consumers is key for developing effective water management strategies and informing infrastructure investments. In addition, both central governments and local water utilities are paying increasing attention to incentive-based approaches and methods for pricing water. In these applications, the price for water should reflect an optimal allocation across alternative uses to maximize the economic benefits of water consumption (Grafton et al., 2020). Proper economic valuation of water resources can, however, be technically challenging and can require large amounts of physical and socioeconomic data (Alamanos et al., 2019). Unfortunately, simple, accounting-based procedures for valuing water resources can lead to “average” value metrics that drastically over- or underestimate the economic value of water, as they do not reflect economic opportunity costs or the true scarcity value of water (Griffin, 2016). Use of such values in policy or management decisions can therefore encourage the inefficient use of the resource.

As the threat of water scarcity increases around the world, the global community is increasingly recognizing the importance of more efficient management and allocation of water resources. To increase efficiency of water systems management, it is critical to begin accounting for the many connections and interdependencies between water networks and other key developmental sectors, such as food production and energy generation. The integrated accounting of these factors is often referred to as the food-energy-water (FEW) nexus and highlights the need for integrated water resources management approaches that account for these linkages (Smajgl et al., 2016). As food, energy, and water resource systems become increasingly connected, it is important to develop and apply analytical frameworks to improve value estimates to inform management decisions and more efficiently allocate water resources.

This methods report outlines a replicable framework for conducting water resource valuation and policy analysis within the FEW nexus. A key feature of this framework is integrating water resource systems (i.e., hydrologic models) with human behavioral systems (i.e., economic models) through a hydro-economic modeling approach. Hydro-economic applications have become more common in recent years. Our goal is to articulate a generalizable, flexible, and geographically portable hydro-economic analysis framework for FEW nexus applications. This report is not intended to describe and assess hydro-economic modeling in general (see, for example, Bekchanov et al. [2017]) or an approach for addressing FEW nexus connections in their entirety. Rather, it is focused on the intersection between the hydro-economic models and the FEW nexus.

The second section provides a conceptual foundation based on natural resource economic theory for the operational approach to water resource valuation. A formal framework for valuing water across sectors and in its different uses is particularly useful for integrated water resources management within the FEW nexus. The third section describes the main elements of an applied hydro-economic modeling framework. We then review the main modeling components and approaches, data requirements, and potential data sources. For hydrologic models, rather than focusing on their inner workings and technical details, we focus on the main input and output features needed to develop an interface with the economic modeling components. For the economic models, we focus on methods and data for representing the economic benefits of water use in different sectors. This section concludes by describing optimization methods that integrate the objectives and constraints from the economic models with the physical constraints defined by the hydrologic models. In the final section, we discuss implications and potential research applications where hydro-economic methods applied to the FEW nexus could be particularly useful.

Conceptual Framework for Economic Valuation and Optimization of Water Resources Within the FEW Nexus

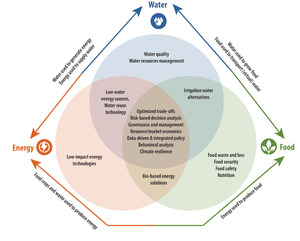
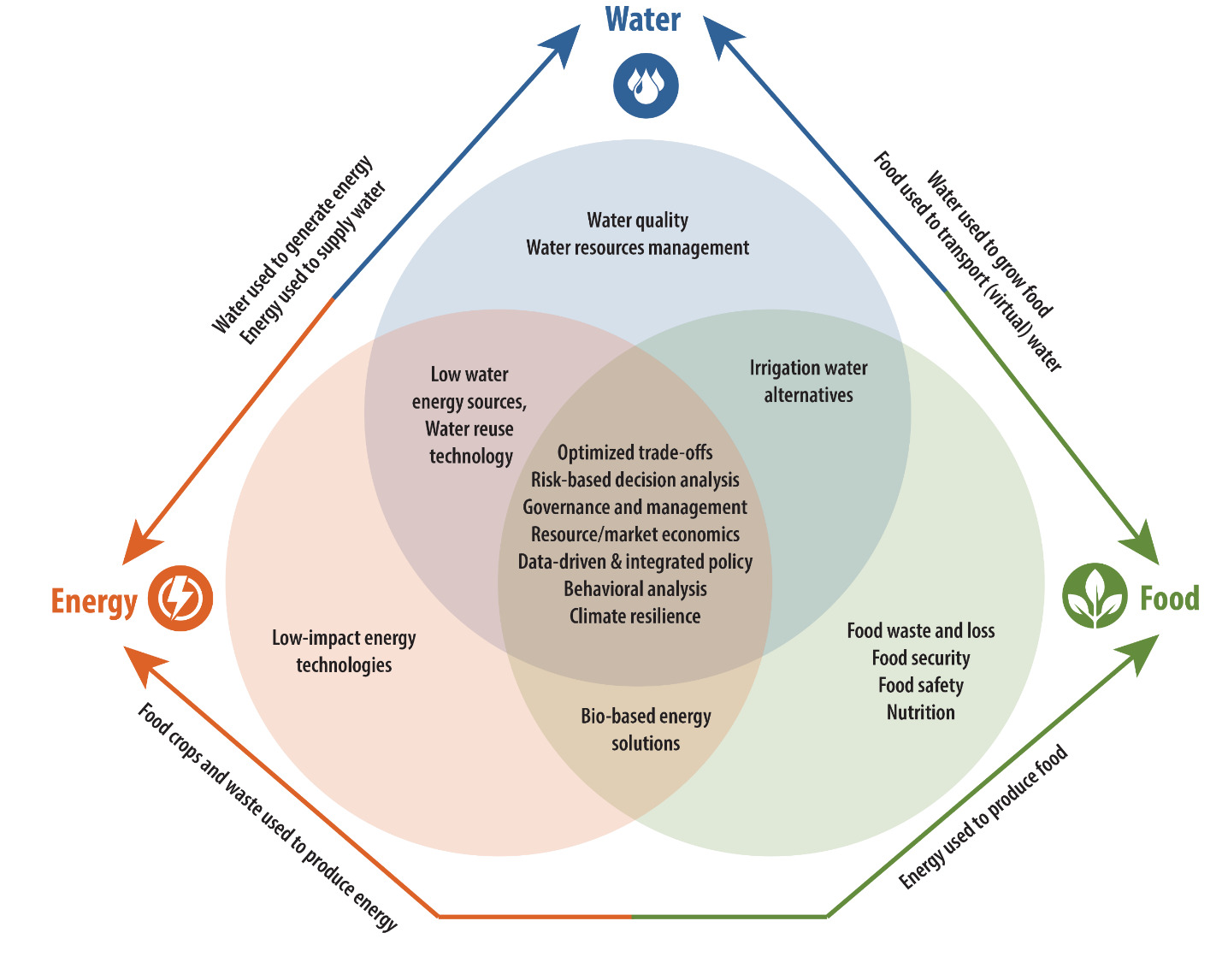
Capturing complex dynamics in the FEW nexus is necessary with growing populations and increased resource scarcity. Originally presented at the Rio+20 Summit in 2012 (United Nations, 2011), the FEW nexus concept is now broadly accepted as an integrated way to address environment and natural resource challenges. Shown in Figure 1, the nexus represents the multiple linkages and interdependencies between water, food production, and energy generation and consumption, which make joint management of these elements both difficult and imperative. Water is needed to produce both food and energy, while energy is needed to transport and deliver water. In many cases, food production and renewable energy production (biofuels) must compete for the same water resources. Accounting for these FEW connections allows for approaches that are more comprehensive and evidence-based, not only for water resource management, but also for strengthening risk-based decision-making, water governance, and climate change resiliency.

Figure 1.The food-energy-water nexus

Analyzing the FEW nexus requires approaches that capture the inextricable linkages presented in Figure 1 and reflect the opportunity costs of allocating water (and energy) for one use at the expense of another. The economic costs and benefits of alternative water uses produce both trade-offs and synergies between water use for energy production, food production, and household and industrial consumption (D’Odorico et al., 2018). Although not explicitly shown in the figure, interactions between land uses (including agriculture) and water resource management are also key in the FEW nexus, as land resources are critical for sustaining food and, increasingly, renewable energy systems. Furthermore, land management changes can affect hydrologic flow and the demand for water.

Hydro-economic models are particularly well-suited for analyzing water resource management challenges in a way that captures many of the key FEW nexus connections shown in Figure 1. They do this by integrating spatially and temporally distributed water resource systems with multisectoral economic valuation methods. As such, they can be used to analyze and, in many cases, optimize water allocation between different uses (including food and energy production) while accounting for physical, economic, environmental, and institutional constraints (Salman et al., 2018). The economic constraints can include other FEW nexus dimensions shown in Figure 1, such as the energy inputs needed for water distribution and food production, or the crop output requirements for biofuel production. Hydro-economic models are applied to a wide range of FEW nexus topics, including the following:

• Country- or region-scale analysis of FEW nexus development and resource management pathways (Kahil et al., 2018)

• Analysis of agricultural and/or water-related implications of renewable energy development (Bekchanov et al., 2017)

• Climate change impacts and resilience analyses (Szinai et al., 2020)

Hydro-economic modeling is well-suited for nexus applications, as the approach captures physical and economic linkages between food, energy, and water systems across space and time. For a review of hydro-economic models and applications, see, for example, Bekchanov et al. (2017), which describes these and other water-economy modeling applications.

In this section, we describe a basic conceptual framework for valuing and optimizing water resources within a hydro-economic model. We begin by defining the term “economic value” and how it can be applied to specific uses of groundwater and surface water resources, including for food and energy production.

Economic Value Concept Applied to Water

The concept of economic value, whether applied to natural resources like water or any other type of physical asset or commodity, must ultimately be linked to people’s preferences and the well-being they derive from the resources, assets, or commodities (Young & Loomis, 2014). In short, water resources have economic value to the extent that humans are willing to pay some price for them. For this reason, to measure economic value in dollar terms, economists most commonly rely on the concept of willingness to pay (WTP)—in other words, what is the maximum amount of income one would be willing and able to forgo? For goods and services that are actively traded, WTP can be directly observed in their market prices. In contrast, many of the benefits provided by water resources are not bought or sold in markets; however, they still provide important economic value. For example, we typically do not have to pay for boating on a lake or drawing water from a private well, but these uses of water have economic value because there is some amount we would be willing to pay for them if we had to.

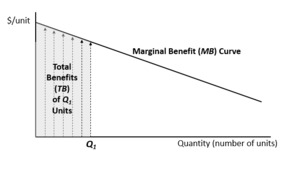
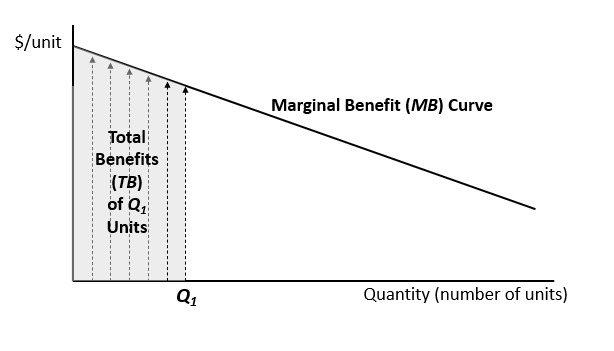
Regardless of how a water resource is used, its value in any particular use can typically be represented by a marginal benefit curve, as shown in Figure 2. The horizontal axis represents the quantity of water used. The height of the marginal benefit curve, shown by the arrows, represents the maximum WTP for each additional unit of water for the specified use (and time period). The marginal benefit curve has a downward slope to represent declining marginal benefit. For example, if water is used to irrigate farmland, the first several units used will have relatively high value (i.e., WTP) for farmers, but the value of additional units will eventually decline as they provide less and less additional benefit to the farmer. If the amount of water used in this specified activity is equal to Q₁, then the total benefit (and hence the total value) of this specific water use is represented by the area under the marginal benefit curve up to Q₁, as shown in Figure 2.

Figure 2.Marginal benefit curve

A related concept is the average value (average benefit) of water. For any quantity of water (Q₁), it can be calculated as the total benefits divided by the quantity—in other words, the average value of Q₁ = TB(Q₁)/Q₁. Clearly this is different from the marginal benefit. Although not shown in Figure 2, in that specific case, the average value of water would always be greater than the marginal benefit (except for the first unit, in which case they would be the same).

The literature on natural resource economics is clear that marginal benefit curves are preferable for use in valuation and other economic analysis contexts; nevertheless, many studies focus on estimation of average value of water using a variety of accounting-based procedures (e.g., Al-Karablieh et al., 2012; Aylward et al., 2010). Average value approaches typically start with some estimate of the total value of the resource or total expenditures allocated to water consumption activities. This total value is then divided by the total amount of water used in that activity during the same period. Sometimes, these values use data from social accounting matrices to assess the value of the output provided by an economic activity and the amount of water used in the production process. Through imputation methods that account for other production inputs, the residual value contribution of the water input can be estimated.

The use of marginal benefit curves in water resource valuation presents many advantages over average value approaches. Average value metrics are limited in a policy setting, as they do not reflect a society’s WTP for the next unit of water or the scarcity value of the resource. Consistent with economic theory, we expect the value of a natural resource to increase with the level of scarcity. As water becomes less abundant, consumers are willing to pay more per unit. This scarcity value is seen in other resource markets, such as minerals and petroleum, where temporary supply shortages lead to increased prices. Because average values for water are generally greater than marginal values (as discussed above in relation to Figure 2, where marginal benefits are assumed to always be declining with respect to quantity used), water resource valuation studies based on average value approaches will typically overestimate the value of water per unit.

Because marginal values reflect water scarcity, marginal benefit estimation can enable water managers to set more-effective price structures and reduce systematic inefficiencies. Marginal benefit curves in the water sector are akin to demand curves—they reflect the price that a society or a single user group is willing to pay for the resource at a given quantity provided. Use of marginal benefit offers an improved method for projecting the implicit price of water. Such information can be critical for establishing rates, establishing tariff structures, or just to recoup government expenditures allocated to water distribution and treatment. An average value approach could provide a value metric somewhere along the marginal benefit curve, but it would not reflect the marginal value of water at the level of current consumption.

In addition to distinguishing between marginal, average, and total benefits, it is important to distinguish between at-source and at-site values for water (Young & Loomis, 2014). Moving water from its source (e.g., from a river or from an aquifer) to its site of use (e.g., a farm field or a household tap) involves costs. As a result, a user’s WTP for water at its source will generally be lower than at its site of use. In particular, the relationship between at-source and at-site benefits can be summarized as follows:

Benefits of at-source water

= (Benefits of at-site water) – (Costs of delivering water from source to site of use)

= Net benefits of at-site water

The costs that drive a wedge between at-source and at-site values can include (1) the fixed costs of infrastructure (e.g., pipes, canals, and pump stations), which do not vary directly with amount of water delivered, and (2) variable costs such as energy and, in some cases, treatment costs, which do depend on the amount of water delivered.

Given this distinction and to avoid confusion, when referring to the value of water, we mainly focus on the benefits of water at its source. It does not include the separate and additional value associated with delivering water to the site of use (water distribution) and treating water before use for improved water quality. The values and costs of water delivery and treatment are not ignored, but they are kept separate and used to define net benefits at the point of use.

When valuing water at its source, it is essential to account for the many ways in which the water can be used or appreciated to support human well-being. To value multiple-benefit natural resources like water, economists often use a total economic value (TEV) framework (Pearce & Pretty, 1993), such as the one shown in Figure 3. The TEV framework for water provides a classifications hierarchy that begins by separating use and nonuse values. In contrast to use values, which are associated with specific human activities that require water, humans receive nonuse value simply from the knowledge that a water resource exists and is being protected. Figure 3 also shows three broad categories of beneficiaries for water-related values. It shows that use values for water can accrue to households, as well as to commercial sector establishment or to public sector organizations. Nonuse values, on the other hand and by definition, can only accrue to households and the individuals who are part of them.

Figure 3.Modified total economic value framework for valuing water resources

In the TEV hierarchy shown in Figure 3, use values are further subdivided into direct and indirect use values. A water resource provides direct use value when the water itself is used or appreciated by humans to produce goods or services or to otherwise support their well-being. It provides indirect use value through its role in supporting the other natural processes or features (e.g., plant and animal life) that humans directly use or appreciate. For example, water that flows into an estuary provides indirect use value to commercial and recreational fishers by supporting the natural habitat for fish they catch. In the framework, nonuse values are also separated into those that are directly derived from a water resource and those that are associated with other natural systems that are dependent on water (e.g., endangered aquatic species).

Direct use values are also separated in this framework to distinguish between consumptive and nonconsumptive uses. This distinction is important because it helps identify uses and values that make it more like a private good (only one user can benefit at a time) and those that are more like a public good (multiple users can benefit at the same time). Table 1 displays the main differences between private and public goods, and those that have characteristics of both—club goods and common resources—and offers a standard microeconomic taxonomy for these types of goods. They are distinguished by two main dimensions: rivalry and excludability. Rivalry means that more consumption of the good by one individual directly reduces availability and consumption of the good by other individuals. Excludability means that access to the good can be restricted to a subset of individuals. Pure private goods are both rivalrous and excludable, whereas pure public goods are neither.

Understanding and accounting for these differences is essential when measuring the total value of a water resource. Consumptive uses are inherently more like a private good by being rival in use—in other words, when one person extracts a water unit for one use, it is no longer available (at that time and location) for another person or another use. In contrast, nonconsumptive uses (and nonuse values) are more like a public good; they do not necessarily preclude other nonconsumptive uses (or nonuse values). For example, water stored in a reservoir for hydroelectricity can also be used for recreation, and multiple recreators can use the same waterbody at the same time. As shown by the example in Table 1, consumptive uses like drinking water and nonconsumptive uses like swimming can be either excludable or non-excludable.

Value and Optimal Allocation on Water

Because of differences in the benefits and costs of water use in different activities, the value of water at its source will depend on how it is used. From the perspective of economic efficiency, the optimal allocation of water is one that maximizes the sum of its total value across multiple uses.

An optimal allocation approach draws from natural resource economic theory and allows one to simulate efficient water allocations over space and time and by endogenous (i.e., model-derived) user groups instead of assuming allocations a priori. In a policy setting, it is often important to assume baseline allocations and existing water management profiles, and optimization models can be calibrated to such assumptions. However, it can be important to consider the TEV of water in the absence of inefficient water management practices, allocations, or pricing structures, especially if the goal of the valuation exercise is to determine the value of a finite stock of water over some specified policy horizon.

Figure 4 demonstrates the concept of optimal water allocation using a simple example involving only two potential consumptive uses—irrigation for agriculture and cooling water for energy production. To simplify, we assume that all water extracted for either use is consumed and not returned to main stock. The width of the horizontal access ($\overline{Q}$) represents the total stock of available water for a specified time period. At this stage, to simplify, we assume that this is a “static” one-period problem. Water cannot be saved for the next period (i.e., use it or lose it), so the issue is how to make best use of the stock in this period. The left-side vertical axis measures the benefit of water for agricultural production, and the right-side vertical axis measures the benefit for energy production. Both measures are expressed as values per unit of water, such as $/m³. The curve MB_A(Q_A) represents the marginal benefit of the water quantity Q_A used for agriculture (measured from left to right on the horizontal axis, similar to the marginal benefit curve in Figure 2). The curve MB_E(Q_E) represents the marginal benefit of water used in energy production; however, the quantity of water used in energy (Q_E) is measured from right to left.

Figure 4.The equimarginal principle: optimal allocation of water across two user groups

The physical water constraint in this one-period case, where the two water uses are mutually exclusive (i.e., each individual unit of water in this case is not a public good that can be enjoyed by more than one user at a time), is that the combined water use in the two sectors cannot exceed the total available stock:

$$Q_{A} + Q_{E} \leq \overline{Q} \tag{1}$$

Under these conditions, the optimal water allocation, represented by the water use combination of Q_A* and Q_E*, is shown where the two marginal benefit curves intersect (i.e., the marginal benefits are the same in the two sectors) and all the available water is used, such that

$${{MB}}_{A}(Q_{A}^{*}) = {MB}_{E}(Q_{E}^{*}) \tag{2}$$

$${Q}_{A}^{*}=\overline{Q} - Q_{E}^{*} \tag{3}$$

At this optimal allocation, the total combined value of water in the two uses is maximized (i.e., the total area under the two marginal benefit curves is maximized). This point also refers to the equimarginal principle, which dictates that the optimal allocation of a finite resource will occur at the point in which the marginal benefits are equal between competing users of the resource.

This one-period optimization example highlights an important trade-off concept for water valuation, which is the opportunity cost of water use. When water uses are mutually exclusive, as in this case, then using a unit of water in one sector means that one must forgo the benefit of using that water in the other sector. This forgone benefit is the opportunity cost. Consequently, the marginal benefit (e.g., MB_A) of water use in one sector can be interpreted as the marginal opportunity cost of use in the other sector. When there are more than two alternative water uses, then the marginal opportunity cost of use in one sector is equal to the highest marginal benefit of water use in any of the other sectors.

This example also helps to underscore an important distinction between two economic value concepts pertaining to water resources:

1. the flow value of water, which is represented by the marginal benefit of each additional unit of the water resource

2. the stock value of the water, the total value of all available units in a given period, which is represented by the area under the marginal benefit curves

For a one-period model, the stock value is maximized when the flow values are equalized across the different alternative uses. At this optimal allocation, the equalized flow value—${MB}_{A}\left( Q_{A}^{*} \right) = {MB}_{E}\left( Q_{E}^{*} \right)$—occurs at the optimal price or implicit price of water.

This simple one-period example can be adapted to include water uses that are not mutually exclusive, in which case water has characteristics of a public good. In this adapted example (shown in Figure 5), we replace the consumptive use (water for agricultural irrigation) with two nonconsumptive uses (hydropower generation and recreational whitewater rafting). These two uses are not mutually exclusive (non-rivalrous) with respect to each other—instream flow used for hydropower can also be used for rafting—but they are both mutually exclusive with respect to irrigation water use (assuming water for irrigation is withdrawn upstream from the point where the other two uses occur). As a result, the marginal benefit curves are additive; in other words, the marginal benefits for rafting can be added to the marginal benefits for hydropower generation. If there were no benefits from recreational use, then the optimal allocation would correspond to point A (where the marginal benefits for agriculture and hydropower are the same). However, with positive recreation benefits, the optimal allocation of water changes from point A to point B, which increases the allocation for energy (and recreation) and decreases the allocation for agriculture, to the point where the marginal benefits for agriculture are equal to the sum of marginal benefits for hydropower and recreation.

Figure 5.Optimal allocation of water with multiple nonconsumptive uses of the same resource

The framework used to conceptualize single-period (static) water allocation decisions can also be adapted to examine multiperiod (dynamic) allocation decisions. In a dynamic context, one must account for and compare values for water services across time. Considering intertemporal trade-offs associated with water use is particularly important when water resources do not replenish themselves quickly (e.g., groundwater resources in arid regions). In these cases, the availability of the resource for future users depends on how much is used in the present.

Figure 6 represents the concept of dynamic optimization in water allocation decisions using a simple two-period example. This framework is very similar to the single-period framework shown in Figures 4 and 5; however, rather than allocating water across two different uses in the same time period, this simple example allocates a single type of water use (human consumption) across two time periods.

Figure 6.Dynamic optimization: efficient intertemporal allocation of a nonrenewable water source in a two-period model with a single type of water use

For simplification, we assume that the resource does not replenish itself, like a groundwater aquifer (i.e., it is a nonrenewable resource), and that the stock of water $\overline{Q}$ is available for only two periods.

One important feature of this dynamic optimization example is that the allocation decision must be made in the current period (period 1). Therefore, for water used in the future, we must consider how much we value those uses in the current period. In other words, we must consider the present value of water use in period 2. To address this point, we apply a conventional “discounting” approach. Under this approach, benefits received (and costs incurred) farther in future periods receive less weight than those received closer to the present. This discounting of future periods is meant to reflect a preference for current consumption over future consumption. This time preference is itself evidenced by the market interest rates that are paid to compensate individuals for their savings (i.e., delayed consumption). There is a lengthy literature examining the conceptual basis, ethical foundations, and appropriate methods for discounting. Discount rates typically range between 2 percent and 12 percent, depending on the institution, country, or context in which the discount rate is applied. A lower rate implies less of a discount on values for future uses of water (or a higher value on potential future use of a resource).

Given this current-period perspective, all the benefits represented in Figure 6 must be interpreted as present values. In other words, the curves ${MB}_{1}^{1}$ and ${MB}_{2}^{1}$ represent the time-discounted values (to period 1) of the marginal benefits of water use in periods 1 and 2, respectively. In this notation, the subscripts refer to the time period in which the water is used, rather than to different types of water use. The superscripts refer to the period from which the water use is being valued. In mathematical terms, the present value in period 1 of the marginal benefits of water use in period 2 can be expressed as:

$${MB}_{2}^{1} = {MB}_{2}^{2}/(1 + r) \tag{4}$$
where r is the discount rate.

In this two-period context, the optimal allocation is the allocation across time periods (Q₁*, Q₂*) that maximizes the total present value of water use. The physical water constraint in this case is that the total water use across the two periods cannot exceed the total available stock $\overline{Q}$, which for simplicity is assumed to be fixed (nonrenewable):

$$Q_{1} + Q_{2} \leq \overline{Q} \tag{5}$$

As shown in Figure 6, the optimal water allocation again occurs where the two marginal benefit curves intersect. In this case, it is where the present value (in period 1) of the marginal benefits of water use in each period is the same.

$${MB}_{1}^{1}(Q_{1}^{*}) = {MB}_{2}^{1}(Q_{2}^{*}) \tag{6}$$

At this optimal allocation, the total combined value of water use across the two periods (i.e., the total area under the two curves) is maximized.

Generalizing beyond this two-period example, we can consider a future involving multiple (even infinite) time periods. These periods are denoted by t, which represents the number of time periods into the future (such that t = 0 represents the current period). We define dynamic efficiency as the path of resource extraction over time that maximizes the net present value of the resource. In this dynamic context, we also define p_t as the “price” of water in period t. This price is assumed to be equal to the nondiscounted marginal benefit of water use in the period.

$$p_{t} = {MB}_{t}^{t}(Q_{t}) \tag{7}$$

The equivalence of price and marginal benefit assumes that, if water users were charged a price of p_t, they would use water up to the point where the marginal benefit of use is equal to the price.

To illustrate the concept of dynamic efficiency, Figure 7 uses the example of a nonrenewable groundwater resource and shows the relationship between price, water extraction, and water stock over time. It depicts and compares two future paths of water use, one of which is dynamically efficient (solid lines) and the other which is not (dotted lines). The optimal price (flow value) and optimal extraction rate are the ones that maximize the long-term value of the groundwater asset (stock value). If the price path is below the optimal rate, it implies that the extraction rate is above optimal, which will lead to rapid depletion of the aquifer. It is also important to note that the true optimal price and long-term average value of water stocks can only be estimated using a dynamic framework that explicitly accounts for trade-offs between current and future uses. Valuation methods based strictly on current average returns from water use in different sectors cannot provide meaningful estimates of groundwater values (Ward & Michelsen, 2002).

Figure 7.Comparison of optimal and inefficient time paths of groundwater extraction

Although seminal research by Gisser and Sanchez (1980) indicated that the economic benefits of optimally managing aquifers are insignificant, that result has been questioned in more-recent studies (e.g., Koundouri, 2004), which gives credence to the use of dynamic economic frameworks for applications of groundwater management policy or water resource valuation. This is especially true for valuation studies—if a policy maker wishes to estimate the total value of the groundwater stock, assumptions of dynamic efficiency are critical, as the full value of groundwater in storage will correspond to a dynamically efficient extraction path.

Simple theoretical models of optimal (i.e., economically efficient) nonrenewable resource extraction have shown that the optimal price path is one where the price of the resource increases over time at the same rate as the discount rate. This conclusion, known as Hotelling’s rule (Hotelling, 1931), is based on several simplifying assumptions (e.g., extraction costs are independent of the available stock); however, it provides basic guidance on the expected time path of prices under optimal conditions.

This basic framework can be expanded to analyze dynamic efficiency under more-complex conditions, particularly when water resources are renewable. If the resource recharges itself naturally over time, the intertemporal resource constraints are relaxed. In that case, the growth of the optimal price path will be less than the discount rate.

Applied Framework for Economic Valuation and Optimization of Water Resources: Hydro-economic Model

Applying this conceptual model for water resource valuation and policy analysis requires an analytical framework that represents and fully integrates natural hydrologic systems and human/economic systems. In other words, it requires a hydro-economic model (Bekchanov et al., 2017; Harou et al., 2009).

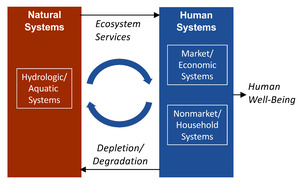
The basic principles of a hydro-economic model are shown in Figure 8. Hydro-economic models account for important connections and feedbacks between human systems (including the economy) and natural hydrologic systems. These frameworks can capture the key contributions that water resources and related natural systems can make to human activities and their well-being. These contributions, also referred to as ecosystem services, support the production of market goods and services (e.g., commercial agriculture and energy generation) as well as nonmarket systems (e.g., household food preparation). Although not specifically shown in the diagram, water resources support public sector non-market production systems (i.e., public water supply). These frameworks also capture how human activities and water uses can affect the quantity and quality of water resources, for example by depleting them through over-consumption, or degrading them through activities that release pollutants into the watershed or augment natural processes that maintain the level or flow of a quality constituent such as sediment.

Figure 8.Representation of an integrated hydro-economic model

Figure 9 provides a more-formal schematic of a hydro-economic modeling framework, in this case integrating a surface water (i.e., river and stream) network with an economic demand module. It begins with basic environmental and socioeconomic data inputs, which then feed the interconnected FEW nexus modeling components, and finally shows a range of outputs and results that can be generated.

Figure 9.Conceptual flow diagram of an integrated hydro-economic model for a surface water system

In this case, environmental data include inputs such as temperature, precipitation, and other relevant climate inputs (e.g., solar radiation); soil types; geophysical characteristics of the landscape; and other factors used to simulate hydrologic flow of a surface or groundwater system. These inputs are typically used to develop a spatially explicit representation of the water resource system over some time series of climate inputs. For example, land use data inputs, such as land area covered by forests, wetlands, cropland, pasture, and urban development, are key hydrology modeling factors for the partitioning of rainfall between surface runoff, evapotranspiration, and infiltration to groundwater. Several proprietary and open-source tools have emerged that allow users to use these inputs to conduct hydrologic simulation (e.g., Hydro-BID, MODFLOW, and Community Water Model).

Socioeconomic inputs are the main data used to parameterize marginal benefit and cost assumptions, as described in subsequent sections. They include information on (1) production costs and prices in the water using sectors, (2) costs and prices for delivering water to these sectors, (3) output prices or non-market values associated with water consumption, and (4) demographic information for the populations being served. Some of the environmental data also provide useful inputs for specifying water demand functions, such as climate and land use data for agriculture.

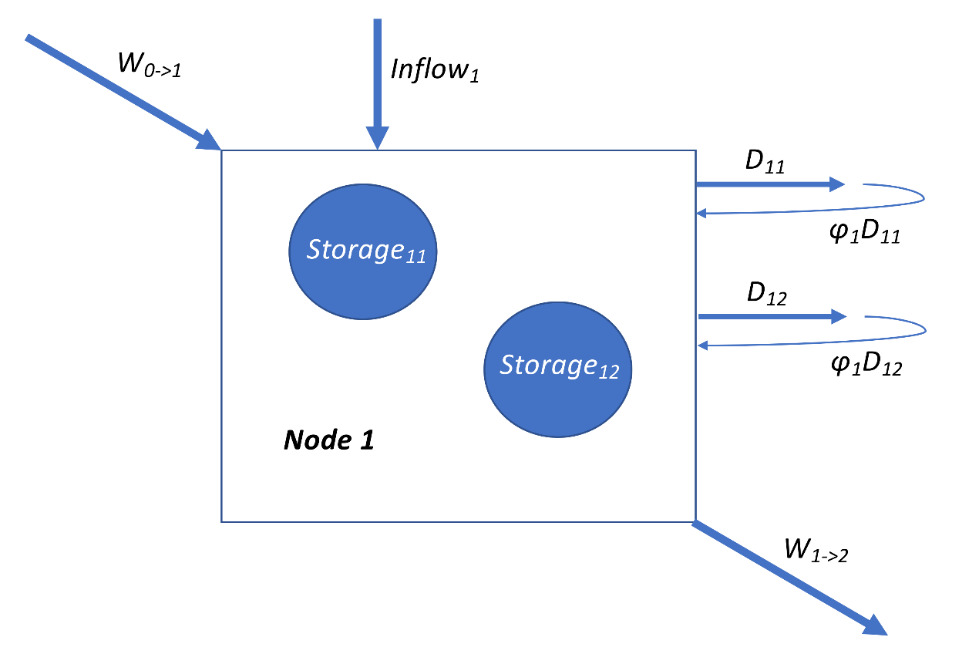
Hydro-economic models typically include a spatial representation of the interconnected hydrologic and economic systems (Herman et al., 2018; Pakhtigian et al., 2021). For example, to analyze surface water systems, a hydro-economic model will typically include a spatial network (node structure) model of river and stream flows representing hydrologic flow from upstream to downstream. Although not shown in Figure 9, hydro-economic models often also incorporate groundwater hydrology by representing the geologic and spatial configuration of aquifers and their recharge/discharge connections with surface systems. These representations of the hydrologic system can be coupled with an economic model specifying the locations of actual and potential human withdrawals, storage, and other uses, as well as return flows to the system.

Depending on the context and analytical needs, these models also often include a multiperiod (i.e., dynamic) representation of these systems and interactions using dynamic optimization methods. Such models treat water resources as a natural asset that must be managed over multiple periods into the future and explicitly recognize how use in one period affects availability and use of water in all future periods. This dynamic approach is particularly important in cases where water is or can be stored over many years, such as in groundwater aquifers or above-ground reservoirs or when the natural rate at which these systems recharge themselves is low.

The key components of the economic model are the representations of the demand (i.e., marginal benefits) functions for water across the different water-dependent sectors. The methods used to generate these functions are described in more detail in the following sections. Globally, the largest consumptive uses of water are for irrigation, energy, and public water supplies (Boretti & Rosa, 2019). Hydropower is a nonconsumptive use of water, but it accounts for roughly 16 percent of global electricity generation (IEA Statistics, 2014). For this reason, our discussion of water demand places the most emphasis on these sectors. Nevertheless, it is important to stress that there are many other valuable consumptive and nonconsumptive uses, including non-energy industrial uses, navigation, and commercial fishing and recreational fishing. Even though they are not discussed in as much detail, many of the same principles discussed in this report for estimating water demand apply to these other sectors.

Several modeling techniques can and have been used to estimate these benefit/demand functions for water in different uses. A detailed review of these methods is beyond the scope of this report (see Young & Loomis [2014], for example, for such a review); however, these methods can be broadly divided into deductive and inductive approaches. Whereas inductive methods typically use micro-level data on human behaviors or preferences to statistically estimate value functions, deductive approaches rely on more aggregate-level data and parameter assumptions to simulate values under alternative scenarios. Both approaches can provide useful benefit information as inputs for hydro-economic models, but because of data requirements, inductive approaches are rarely directly incorporated into hydro-economic models—rather, the results or parameter estimates (e.g., demand elasticities) from applying these methods are used.

Once the demand functions are specified, hydro-economic models aggregate these components to evaluate the relative costs and benefits of different feasible allocations of water across sectors, time, and space. In many cases, they also include an optimization framework designed to select the allocation that provides the highest total benefits to all users combined.

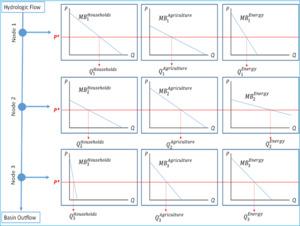
Figure 10 provides a conceptual example of this approach. Assuming hydrologic connectivity from nodes 1–3 (upstream to downstream), a hydro-economic model will ideally represent marginal benefit curves separately for different sectors (households, agriculture, and energy) and spatial nodes. This example shows that the curvature of the marginal benefit functions can vary spatially, depending on the locations of existing infrastructure; populations; and other factors, such as marginal productivity of water as an input to agricultural production and other processes. An optimal solution would thus establish an allocation with an implicit price on water (p*) that is equal across space and user groups, though many environmental and institutional factors could make such an allocation difficult to achieve.

Figure 10.Conceptual schematic of a hydro-economic model that represents hydrologic flow from upstream to downstream and marginal benefit curves that are differentiated by sector and across space

Note: Subscripts for MB and Q refer to node.

Hydro-economic models have the flexibility to evaluate a broad range of scenarios of interest, including the following:

• Potential management solutions to resolve conflicts between various user groups (e.g., irrigators and households): for example, models can specify alternative water allocation rules or constraints in the model and analyze the cost-benefit and water balance implications.

• Infrastructure investment options (including new reservoirs, water transfer projects, or water saving irrigation technologies): models can optimize water allocation under scenarios with and without the investment options and compare the total benefits of water use across scenarios.

• Climate change projections and adaptation analysis: for example, models can run the hydrologic and water demand components of the model under alternative temperature and precipitation conditions.

• Changing demographic or economic projections.

• Alternative water management approaches or institutional reform (including use of water markets or mandatory protection of in stream flows): for example, optimization can be used to replicate water use outcomes and efficiency gains associated with perfectly functioning water markets, and instream flow protections can be modeled by including these flow requirements as constraints in the optimization.

Hydro-economic analysis at the basin, region, or country scale can reveal important economic and physical outcomes across different scenarios. The approach allows for a direct comparison of economic benefits across alternative uses to determine the optimal combination of infrastructure investment and management of water over space and time. Furthermore, economically optimal outcomes can lead to significant changes to the hydrograph of a watershed or depletion trajectory for an aquifer, which could alter seasonal water supplies and economic opportunities across space or in future periods (Baker et al., 2016). Hydro-economic optimization allows for detailed scenario analysis to assess key trade-offs across market and nonmarket water uses associated with optimal allocation schemes (Momblanch et al., 2016).

The following sections provide additional details on how data inputs for key components are developed and integrated into hydro-economic models. This includes information about the hydrologic system being analyzed (e.g., watersheds or groundwater systems) and sector-specific information on how marginal benefits (and marginal costs) can be evaluated for different sectors. Furthermore, we describe the general architecture of a hydro-economic optimization model, including the necessary hydrologic inputs and other geospatial and economic data layers needed to develop such a model.

Watershed Surface Water Hydrology

Any model used to estimate the value of water from some resource base or to conduct policy experiments to evaluate the effectiveness of conservation efforts or alternative pricing schemes must be grounded in sound hydrology. For example, a hydrologic model could begin with a generic hydrologic modeling structure that supports the development of an economic optimization model to evaluate optimal allocations of water.

For surface water systems, one approach involves compiling various geospatial layers and analytical hydrography datasets (AHD) that capture pristine (natural) inflows through the watershed. Example frameworks developed and applied by coauthors of this report include proprietary tools such as WaterFALL^TM (Eddy et al., 2017), which was developed for application in the United States and takes advantage of the existing data in the National Hydrography Dataset Plus (NHDPlus) (US Environmental Protection Agency, 2019), and the publicly available Hydro-BID modeling system (Moreda et al., 2014), which was developed with Inter-American Development Bank for Latin America and Caribbean and required development of a specific AHD for this region based on lower-resolution data.^[1]

To develop watershed schematics representing the flow and allocation of water over space and time, hydrology and climate analysis modules can be used to estimate the availability (volumes and fluxes) of fresh water at the regional, basin, and sub-basin scales. For example, the primary hydrology component of WaterFALL^TM and Hydro-BID is based on the Generalized Watershed Loading Function (GWLF) modeling framework (Haith, 1985; Haith et al., 1992), shown in Figure 11, and enhanced by a lag-routing methodology (Moreda et al., 2014).

Figure 11.Schematic representation of the GWLF Model

Source: Modified from Haith et al. (1992)

For surface water simulations, the rainfall runoff model component of GWLF is applied on AHD catchment units by accounting for the land uses and soil conditions within the catchment on a daily time step. The response of each land use in a catchment is treated separately to generate an estimate of runoff volume. The flow generated from each catchment, including shallow groundwater contributions or base flow, is routed through stream networks defined by the AHD. The distributed model architecture provides a high level of scalability.

Most of GWLF’s required parameters for estimating surface water flows are assembled in a database for each of the AHD catchments, including catchment area and stream length. Table 2 describes the main parameters of GWLF. Calibration of the model entails scaling the assembled parameters by comparing the model simulation results with observed flows at selected sites.

When observed flows at gauge stations are not available, remote sensing data and regional parameterization methods can be used to improve input data and calibration techniques for hydrologic modeling in data-scarce regions. Developing a hydro-economic model will require data inputs that are not constrained by local availability. It is important to identify the best available datasets that can be used for this purpose. These datasets should cover global areas and should be of an appropriate spatial resolution to run on the AHD network. Additionally, methods need to be developed to expand model calibration options to best represent pristine flows in the absence or limitation of gauged stations within a study area.

One potential method outlined in Sagintayev et al. (2012) and Peng et al. (2006) is to use remote sensing satellite data to derive changes in reservoir volumes. Many other studies have used remote sensing data for input data parameters. Xu et al. (2014) summarizes how remote sensing data has been integrated into hydrologic modeling. In many cases, remote sensing data can be used to identify basin inputs (boundary, digital elevation maps), data assimilation (model constraints based on observations), and, to a lesser extent, model calibration. This paper includes a variety of remote sensing data sources that can be used for model input parameters and the relative pros and cons of the sources. The paper includes sources of information for precipitation, soil moisture, snow cover, and evapotranspiration. Regardless of the calibration procedure, development of the hydrologic framework will yield spatial layers that capture hydrologic continuity over time for all time periods (e.g., days or months) with available climate data.

Once the general hydrologic framework and dataset are assembled, development of a watershed or groundwater schematic for the economic model involves grouping subcatchment scale flow data to the appropriate geographic area and time. Model developers will choose the relevant temporal or spatial scale for the application of interest. For a watershed-scale hydro-economic model, it is often appropriate to aggregate to the monthly time step, which is reasonable for capturing both economic costs and benefits of water consumption activities (which are not typically represented at a daily step); to reduce variability in inflows caused by storm surges; and to simplify the optimization process. For a dynamic optimization model of groundwater management, it may be more appropriate to represent water balances and economic benefits at an annual time step, as these typically involve longer-term simulations spanning multiple decades.

Appropriate spatial aggregation of a model requires consideration of several key factors, including the following:

1. Location of major reservoirs or water storage/distribution infrastructure

2. Locations of key withdrawal or consumption points (cities, farms, etc.)

3. Water, energy, or food demands by source (preferably seasonal demands)

4. Information on water distribution/transport infrastructure to end use (including efficiency)

5. Return flow proportions

6. Recharge if available for ground water

7. Smallest administrative unit for which economic data are available

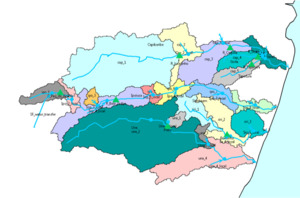
As an example, consider a recent economic valuation analysis conducted in Northeast Brazil. Figure 12 shows the geographic extent of four adjacent river basins in Pernambuco, Brazil. This map shows how AHD sub-catchments (with gray boundaries) are aggregated spatially to represent a complete watershed. If economic data were available at a fine spatial resolution and water was consumed consistently over the geographic area, then a hydro-economic model could have been developed based directly on these primary subcatchments. Instead, for this example, subcatchments were aggregated into larger geographic units that were consistent with how water is stored and distributed within Pernambuco.

Figure 12.Example of a watershed-based hydrologic network, including four basins in the State of Pernambuco, Brazil

Note: Gray lines show AHD sub-catchment boundaries.
Source: Baker et al. (2016).

Specifically, the AHD subcatchments were grouped into 21 larger catchment spatial units (nodes) based on locations of key reservoirs and surface water demand networks (as displayed in Figure 13). Each colored area represents a separate node. For instance, the “cap_1” node in Figure 13 is larger than other spatial units, but it represents an area that is less populated with limited agricultural withdrawals, so it is still only one node. This is also the location of a large storage reservoir (shown as a green triangle) that captures upstream inflows for distribution to various municipal demand points located in downstream units.

Figure 13.Aggregated node schematic of the four basins in Pernambuco Brazil

Source: Baker et al. (2016)

A node network, such as the one shown in Figure 13, provides a simplified representation of the surface water system and a basic structure that can then be used for analyzing water balance and allocation scenarios. The node schematic for this application was developed using the Water Evaluation and Planning Model; however, an alternative system—WaterALLOC (https://www.rti.org/focus-area/wateralloc)—is fully integrated with Hydro-BID, and AHD is now also available for these types of applications.

Thus, once hydrologic flow networks and data are assembled, geospatial analysis tools can be used to develop simplified node schematics and to aggregate flow data accordingly. Modeled flow estimates at the node level and the desired time step can then be used to analyze different water use and management scenarios and to conduct optimization analysis. When building hydrologic inputs for a hydro-economic model, it is often necessary to aggregate data spatially and temporally. In the example provided by Figure 13, local river flows and climate inputs (temperature and precipitation) were aggregated to a monthly time step and a sub-basin level.

Groundwater Hydrology

Representing groundwater hydrology in an economic optimization model is often difficult because of data limitations and complex functional relationships needed to capture lateral flows, recharge rates, and pollution concentration dynamics (including saline water intrusion and nitrate leaching).

As with analyzing watershed hydrology, our approach begins by subdividing a larger area into distinct spatial units. However, whereas the previous procedure is developed to simulate pristine inflows and hydrologic continuity through the system, spatial disaggregation for a groundwater model is needed to subdivide a larger area into smaller units with relatively homogeneous aquifer characteristics. Aquifer characteristics typically vary greatly because of soil porosity and other geologic characteristics, so it is important to capture this heterogeneity to the extent that data are available.

To model groundwater extraction and depletion effects, key parameters typically include

1. distance from ground level to water table,

2. specific yield, and

3. saturated thickness.

Specific yield is an aquifer parameter (expressed in percentage terms) that estimates the approximate amount of water that will drain under the influence of gravity. This parameter defines the proportion of water that is available for consumption from a defined aquifer volume. The saturated thickness is the vertical thickness (measured as a distance) of the aquifer in which pores’ spaces are filled with water.

To the extent that these parameters have been estimated through well sampling and other means, these data can be used to calculate existing groundwater stocks and other initial conditions for the system. In many regions of the world where groundwater depletion is a concern, one can typically find published literature, proprietary data maintained by government agencies, or gray literature that has standard information or maps of key aquifer characteristics. In the absence of such data, one can use Gravity Recovery and Climate Experiment (GRACE) satellite imagery (Abiy & Melesse, 2017) or other means to estimate groundwater storage.

A standard dynamic economic optimization model of groundwater consumptions will include a state equation that conveys depletion dynamics for the system. Equation 8 provides an example:

$${Stoc}k_{j,t + 1} = {Stoc}k_{{jt}} + {Recharg}e_{{jt}} - \sum_{g = 1}^{G}w_{{gjt}} \tag{8}$$

The total stock of groundwater over time is an important model output. For any spatial unit j, the total stock of groundwater available (expressed, for example, in cubic meters) (Stock_jt), will evolve over time as water is consumed. For each time period, the amount of water available is the previous period’s stock, less total water consumption in the previous period for all g = 1…G user groups ($\sum_{g = 1}^{G}w_{{gjt}}$), plus any recharge in the previous period (expressed, for example, in cubic meters per day). The parameter Recharge_jt can represent naturally occurring or manmade recharge.

Furthermore, we can use the specific yield (SpYield) and saturated thickness parameters to simulate pumping lift dynamics over time, which are a key determinant of marginal extraction costs. As water is consumed at rates that exceed the recharge rate, the stock of each aquifer section declines. Pumping lift (Lift_jt), or the difference in distance between the surface area and the groundwater table for spatial unit j at time period t, is inversely related to the groundwater stock. Pumping lift increases over time as more water is consumed, as defined by the following relationship:

$${Lif}t_{{jt}} = {Lift}_{j,t - 1} + \frac{\left( \sum_{g = 1}^{G}w_{{gjt}} - {Recharg}e_{{jt}} \right)}{{SpYiel}d_{j}*{Are}a_{j}} \tag{9}$$

Marginal extraction costs for groundwater are a function of the pumping lift, the total water extracted, the energy required to pump the water, and the price of the energy input:

$${ME}C_{{jt}} = f(E_{{jt}},{Lif}t_{{jt}},\sum_{g}w_{{gjt}},P^{E}) \tag{10}$$
where $E_{{jt}}$ is the energy required to pump groundwater and P^E is the energy price. Using the functional relationship defined in Zhu et al. (2007), we can define the energy requirements for groundwater pumping by the following equation:

$$E_{{gjt}} = {Gravity}*\gamma*\rho*w_{{gjt}}*{Lif}t_{{jt}}\ \forall \ g,j,t \tag{11}$$

Here, Gravity is the acceleration of gravity (9.8 m/sec²), $\gamma$ is pump efficiency (which will vary by irrigation system), $\rho$ is the density of water (1,000 kg per m³), and the endogenously determined pumping lift (from pump intake to ground level). Marginal extraction costs are thus the price of energy (P^E) paid by water users (which can vary by region, over time, and by fuel source), multiplied by total energy consumed to pump groundwater at a specific depth. Furthermore, it is important to note that energy for groundwater extraction is sometimes subsidized, so a water valuation exercise could consider extraction costs under two scenarios—one with subsidized energy costs and one with unsubsidized costs reflecting true marginal extraction costs of the groundwater resource.

Agriculture Sector Benefits

The benefits of water withdrawals by the agricultural sector, including water for crop irrigation and livestock watering, are a main example of a consumptive use value in the TEV framework.

To derive marginal benefit curves for agricultural crop water use, a necessary first step is to understand the amount of water required to grow a particular crop per unit area (e.g., in cubic meters per hectare per month). These crop water requirements link biophysical parameters of crop growth cycles under assumed growing conditions (topography, soil type) with information on climate patterns (including temperature, precipitation, and evapotranspiration) to determine the amount of additional irrigation water that would be required to achieve some desired yield level given observed precipitation inputs. Desired yield levels could include maximum agronomic yield for a particular region/crop or profit maximizing yield. Livestock water requirements have a similar interpretation—for a specific animal type to maintain body weight and/or produce milk, a specific volume of water intake is required. Livestock water requirements can vary by animal type, climate conditions, and feeding regiment.

A standard Food and Agricultural Organization (FAO) approach (Steduto et al., 2009) can be applied to estimate crop water requirements, which are expressed and estimated as a function of crop evaporation, crop water needs, crop-specific irrigation response factors, and agronomic yields. Other methodologies, including Global Yield Gap Atlas (http://www.yieldgap.org/), provide similar templates for estimating crop yield response to water for specific crops. These approaches can be used to estimate crop water requirements for a given day, week, month, or year, given various climate and biophysical inputs, including

• global radiation (MJ/m²/day),

• air temperature (Celsius, min and max daily values),

• relative humidity (min and max daily values),

• wind speed (average m/s), and

• precipitation (mm/day).

In addition to providing crop water requirements expressed as a constant value per hectare for a defined crop yield, these approaches can be used to estimate water response functions for an annual time step. These response functions, also referred to as crop production functions, relay net yield as a function of total irrigation (given specific climate conditions).

Estimating production functions and/or crop water requirements offers several advantages. First, one can link water requirements with marginal costs of withdrawal/extraction curves to represent total costs of irrigation. This is key for determining the net marginal benefits of water at the point of use in agricultural production, which in our framework are tied to economic rents (profits) from crop and livestock production less irrigation costs. Development of profit functions is a central part of our valuation methodology, and requires the following data sources:

• Crop production functions or crop/livestock water requirements

• Producer prices by crop/region (can supplement with national/global prices if data are limited)

• Production costs by crop/region (in data-limited environments, this can require expert judgement from local stakeholders or cost estimates transferred from literature or other regions with similar environments)

Second, this approach can be extended to most cropping systems in the absence of historic data on production and yields. To the extent that historic production levels were based on inefficient or minimal irrigation practices, this offers a way to measure benefits of new irrigation projects that assume efficient irrigation practices. This advantage is important in contexts that seek to define benefits and costs of irrigation expansion projects to improve climate resilience of agricultural systems.

Third, crop production function approaches can be spatially disaggregated to align with existing climate and biophysical data, or to align with maps of existing irrigation infrastructure, such as the FAO Global Map of Irrigation Areas. Given sufficient climate data, the approach can be easily replicated for different countries and administrative zones.

Finally, production functions or crop water requirements depend on climate input, meaning we can easily estimate new parameters under different observed or projected climate conditions. The proliferation of climate data allows for replication of a standard FAO approach across most regions of the world. Furthermore, with existing climate change projections archives (such as from the Climate Model Intercomparison Project), one can develop climate inputs based on projections from Global Circulation Models. This facilitates future climate change impacts and adaptation analysis where water requirements will change on the basis of the projected differences in key climate inputs.

Marginal Benefits in Agriculture

There is a lengthy literature describing various approaches for quantifying economic benefits of irrigation water. The most-common approach is to include a continuous crop production function for each crop, relating per hectare water use and per hectare yield. This is advantageous because it allows for a smoother depiction of the marginal benefit curve as water supplies increase. Here, in addition to total area being an endogenous variable, the amount of water applied per unit area (and by crop) is also endogenous. The production function approach is useful for hydro-economic modeling of FEW nexus issues, as it can be used to calculate spatially explicit profit conditions for different crops and irrigation intensity levels. Production possibilities and profits for different levels of irrigation and crop-mix strategies reflect implicit marginal benefit curves for agriculture in a hydro-economic modeling setting, and costs associated with irrigation water supply and distribution plus system maintenance represent marginal costs. A hydro-economic approach with production functions allows for analysis of intensive and extensive margin shifts in irrigation caused by resource constraints or other scenario-specific factors, which is important in a nexus context where both land and water resource demands may vary across user-defined scenarios. Further, this approach allows for direct incorporation of energy requirements and associated costs for irrigation water supplied from surface and groundwater sources.

A hydro-economic model will determine the amount of land dedicated to different crops (pending user-defined constraint sets). Pending physical availability of the resource, irrigation response functions allow the model to supply additional irrigation water to specific crops in specific model nodes to improve productivity and profitability. A hydro-economic model can either represent irrigation response functions directly, or it can include multiple crop water requirement thresholds that vary by time step, crop, irrigation intensity, and spatial unit (e.g., rainfed yields and water requirements and yields for different levels of irrigation intensity). Yield-response functions can include linear forms such as in Vaux and Pruitt (1983) or non-linear function following a standard FAO methodology (Smith et al., 1998). Open-source software tools such as CROPWAT (Smith, 1992) can be used to estimate irrigation response curves. More generally, the shape of marginal benefit curve will depend on the shape of the individual crop production functions included.

Using any of the approaches described above, the agricultural production possibilities (and the implied marginal benefits) for each crop can be represented and directly introduced into the hydro-economic model, such that the model endogenously picks irrigation rates, crop mixes, and total land use (subject to various constraints) along with water uses in other sectors. This is ideal for models with a sub-annual time step, where additional detail is needed on how model outcomes (e.g., optimal crop mixes and land management) respond to sensitivity analysis or to alterations of key model parameters (e.g., climate inputs).

The choice of modeling approach for representing marginal benefits in agriculture depends on data availability and research budget. The FAO resources described above provide basic components and default values that can be used for simple, constant water requirement applications in most areas across the world. The more-complex approaches will typically require more region-specific data on soil quality, climate inputs, crop yields, and yield-response relationships. Similar water requirements can be developed for livestock using publicly available resources.

Energy Sector Benefits

As discussed, there are complex interactions between water management and energy systems. Thus, it is increasingly important to model economic decisions within these sectors simultaneously. Generating electricity relies on adequate and consistent water supplies, though it is important to distinguish between consumptive and nonconsumptive uses of water use for electricity generation when representing marginal benefits from energy generation activities within a comprehensive modeling framework. The following sections offer insight into how the marginal benefits of water for energy generation can be directly or indirectly represented in an optimization modeling framework.

Hydropower

Economic benefits to hydropower production are best represented by the net revenue created through hydropower generation, though there is sometimes an economic opportunity cost associated with hydropower generation worth considering in a broader economic modeling context. Hydropower is generated through primarily nonconsumptive use of water, as the proportion of water lost or consumed is a small fraction of the inflows that reach a hydropower reservoir. However, although net consumption is small, hydropower generation can alter seasonal hydrographs, which can affect downstream populations and ecosystems. Depending on reservoir operating rules in periods of low flow, hydropower storage to maximize storage height (a key determinant of total energy output) can reduce outflows and limit water consumption options for downstream riparians. A hydro-economic model can explicitly capture these opportunity costs.

Thus, although the economic benefit of each unit of hydropower is usually the same within a model (represented by the electricity price received less costs per unit of electricity), when included within a hydro-economic optimization framework, they allow one to explicitly consider the potential opportunity costs associated with hydropower operating rules, especially during dry seasons or in water-scarce regions. Conversely, there are situations where hydropower infrastructure can help regulate seasonal flows in a manner that complements other economic sectors. In some regions, for instance, adding hydropower reservoirs can help boost irrigated agricultural productivity by regulating flow and ensuring adequate water supplies in the dry season (Lacombe et al., 2014), or can offer flood control benefits during the wet season (Jeuland et al., 2014).

For modeling purposes, several reservoir-specific parameters need to be included for adequate representation of hydropower generation capacity within a system. Operational guidelines for hydropower generation can be developed from existing data on daily generation levels and flow rates. Within a system, each dam should be represented by a common set of parameters:

• Reservoir capacity

• Turbine height

• Turbine intake height

• Generation capacity

• Surface area and evaporation rates

• Spillway height and capacity

• Flood control measures

Typically, these data would be provided by in-country experts and energy sector stakeholders. Sometimes, however, such information can be found in publicly available project planning documents.

In a simplified framework, the hydropower production in period t at a hydropower facility can be modeled as proportional to the product of two factors: (1) average head (difference between reservoir and tailwater elevations) and (2) water flow in period t. If the average head, per unit price, and per unit production costs are assumed to be constant, then the marginal benefits of water flow are constant (i.e., flat). However, because allowing more water to flow through the dam will reduce the head height, this will cause the marginal benefit curve to decline with water flow. This suggests that water stored in hydropower reservoirs produces two sources of economic benefits—(1) the storage benefits of maintaining reservoir head height, and (2) the flow benefits of water.

There are many options for evaluating optimal operating rules at individual reservoirs under different climate conditions and at a fine temporal scale. However, the modeling framework outlined in this report is ideal for evaluating a cascade of dams within a single watershed, and it is best suited to an aggregated temporal scale (e.g., monthly). By capturing hydropower generation and reservoir operations at multiple dams simultaneously, our framework allows for

• evaluation of alternative management and planning options across multiple dams,

• cost/benefit analysis of new hydropower infrastructure investments, and

• analysis of effects of changing environmental conditions (climate change, sediment buildup, etc.) on system-wide hydropower output.

Modeling a cascade of dams as opposed to individual reservoirs also allows us to compare the net economic benefits of system-wide management of water resources relative to a case with no or partial cooperation, following the approach outlined in Jeuland et al. (2014). The trade-off of this approach is that one loses temporal detail with an aggregated modeling approach, so this may not be ideal for problems meeting daily energy load targets or pricing.

Furthermore, with hydropower, it is also important to recognize that the marginal benefits might be represented by avoided costs of more-expensive energy generation options. If hydropower is the lowest-cost source of electricity within a system, then rather than using a constant price to represent the marginal benefit of hydropower generation, one might need to assess the costs of supplying energy from alternative sources. Figure 14 provides a simple conceptual schematic relating electricity generation capacity by source and the marginal costs of generation. If hydropower generation is increased beyond the current demand level, then it would first displace and avoid the marginal costs of alternative energy source 1. If increased enough, it could then begin to displace and avoid the even higher marginal costs of alternative energy source 2.

Figure 14.Hypothetical relationship between the marginal costs of electricity generation and capacity, by source

In general, analysis of incurred energy costs from alternative sources in the presence of resource constraints can require more-sophisticated modeling of energy supply systems that captures not only average cost differences between technologies but also distribution systems challenges and associated costs and temporal considerations that can limit a system’s ability to readily switch between energy sources. Electricity dispatch modeling that connects electricity generation, storage, distribution, and demand systems could be required to evaluate energy sourcing decisions in in the presence of climate anomalies or other scenario factors driving resource shortages.

Although most hydro-economic models can represent energy supply and demand systems within a case study region (and, hence, marginal benefits and costs of energy) in aggregate, such approaches typically do not represent full energy dispatch systems. Although recent advances have been made in representing hydrometeorological uncertainty on energy markets and generation in coupled models (Su et al., 2020) or have linked energy and water dispatch systems (Santhosh et al., 2014), challenges remain in linking real-time dispatch modeling with FEW nexus-focused hydro-economic modeling. In particular, capturing production cycles for land use and agricultural systems typically involves temporal aggregation and intertemporal decision-making at monthly, annual, or multi-year time steps, which is inconsistent with some dispatch models that represent decision points at smaller time steps.

Hydropower reservoirs provide a range of other benefits beyond energy generation that can be incorporated into hydro-economic models. These benefits include flood control protection (Jeuland et al., 2014; Wallington & Cai, 2020), water storage for household distribution, and various recreational opportunities. Hydropower generation can also regulate downstream flows, improving seasonal water availability and complementing downstream agricultural production (Lacombe et al., 2014). Hydro-economic models can also represent the costs of hydropower generation, including fixed capital costs, variable operation and maintenance costs, and capital depreciation costs. Each unit of hydropower could also represent an opportunity cost associated with the forgone benefits from keeping that unit of water in storage.

Thermal Electricity

Like hydropower, the marginal benefits of water used in thermal energy are reflected both by the value of the electricity generated and by avoided costs of alternative generation technologies that are more costly in times of water scarcity or when regulations on water quality (e.g., water discharge temperatures) constrain generation. Like hydropower, thermal energy can provide base load electricity, though this can require a consistent supply of water for cooling purposes. Depending on the system (i.e., once-through or closed loop), water allocations for thermal electricity can be substantial, though net consumption can represent a relatively small share of total withdrawals. Hydro-economic modeling can capture a system of thermal electric facilities sharing a common water resource system, with each facility making withdrawal decisions to maximize total system benefits given regional electricity demands and various cost considerations.

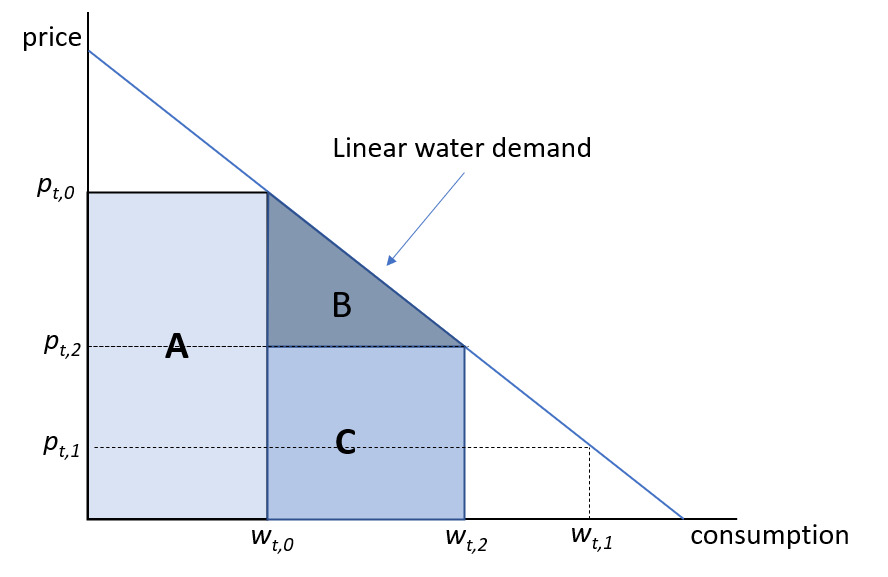
Thermal electricity requires water for cooling, and individual facilities are sensitive to both water availability (supply) and quality (in particular, temperature). Unexpected disturbances to water availability (including drought) can reduce energy generation capacity at a given facility. Like water availability, stream flow temperatures can be highly variable and will depend on a variety of climatic, geographic, and socioeconomic factors. As the temperature of water intake is directly related to the quantity of water needed for the cooling process, so uncertainty in this factor can also influence daily and long-term management decisions for utilities (Van Vliet et al., 2012). Figure 15 displays the facility-level effect of a shift in water temperature. Assuming warmer intake leads to additional costs to cool discharge water (e.g., use of retention ponds), marginal costs will increase from ${c\left( q_{t}^{e} \right)}_{1}$ to ${c\left( q_{t}^{e} \right)}_{2}$, where i refers to facility, j refers to process, and t refers to time period. This shift would result in higher total costs and a reduction in producer benefits, indicated by area ABC.

Figure 15.Marginal cost shift caused by a change in water intake temperature

A framework that captures both water requirements for energy generation and potential water quality impacts of discharge (e.g., thermal water quality) can represent benefits through both the price received by suppliers and the avoided costs of purchasing energy from the grid to make up for supply shortages or periods of excessive costs driven by water availability and temperature. Furthermore, because the energy system is connected to the larger water management system in the modeled region, we account for the opportunity costs of allocating water for cooling in lieu of some alternative use. It is possible that this framework could result in a different implied energy generation mix if current water allocations are less economically beneficial than an alternative allocation scheme that relies less on water for thermal energy. Thus, an optimization modeling framework is ideal for evaluating water and energy management choices in conjunction.

Renewable Energy Expansion and Associated Resource Demands

Renewable energy sources are pivotal points of connection and resource competition within FEW frameworks. Biofuels or bioenergy production from dedicated energy feedstocks can compete for land with primary agricultural products used for food, and their net water impacts can be substantial (Cai et al., 2018; Jeswani et al., 2020). Bioenergy can also be produced from waste material or co-products such as sugarcane bagasse, which can create an additional source of benefits for agricultural producers and drive irrigation water demand. Hydro-economic models can introduce biofuels as an alternative cropping choice, or (more frequently) can introduce constraints requiring a certain amount of feedstock production in an area to hit some policy target. Sensitivity analysis of biofuel requirements in hydro-economic models can be used to compare economic benefits, costs, and resource requirements of alternative biofuel scenarios.

Non-bioenergy renewable resources such as wind and solar do not directly consume water to generate energy, but they require land resources and, in some contexts, could compete directly for land access with food systems. Recent integrated assessment models point to large land resource requirements for wind and solar energy production to achieve ambitious climate change stabilization targets (Shukla et al., 2019). Although these concerns are certainly valid in aggregate, what is less certain is how isolated FEW nexus systems will respond to continued renewable energy development. Baker (2011) shows that land-based climate strategies can reduce water consumption at a country scale, but they may exacerbate local resource scarcity or quality concerns if competition for land drives intensity in water use. More spatially refined analysis of renewable deployment, coupled with hydro-economic analysis, can reveal important trade-offs associated with renewable energy.

Recent integrated analyses of energy and water systems include geospatial frameworks to assess renewable energy expansion potential (Wu et al., 2017). These frameworks typically link spatial and economic factors to estimate the costs of energy expansion for different technologies across space and time. Spatially explicit energy expansion planning models combine climate, hydrologic, land use, and other spatial factors to identify spatial hotspots for renewable energy investments and can be used in policy assessments of on- or off-grid renewable energy policy goals. Such information can be incorporated into broader hydro-economic models, along with resource requirements and marginal benefit/cost specifications for FEW nexus analysis of multiple development objectives.

As an example, Figure 16 provides data visuals representing levelized costs of alternative renewable energy sources in Guatemala using the Spatially Explicit Electricity model for Renewable Energy (SEERE) (Henry et al., 2021). SEERE is a spatially disaggregated energy expansion tool that can be used in a planning or policy context to evaluate energy generation potential and costs while recognizing resource constraints. Such cost information is important for assessments of spatio-temporal allocation of resources to meet various policy objectives in the FEW nexus.

Figure 16.Estimated levelized costs of energy for alternative renewable sources

Note: (A) solar and (B) wind energy throughout Guatemala, and (C) micro-hydro in the Pacific Lowlands watersheds. LCOE = levelized cost of electricity.

Household Consumption Benefits

Household water use (also referred to as domestic or residential water use) also accounts for a significant portion of water withdrawals in most countries and, correspondingly, a significant portion of its direct use value. For example, domestic use accounts for roughly 15 percent of withdrawals in the United States (Maupin et al., 2014). Like water used for irrigation, it is a private good, which means that domestic use reduces water available for other uses. Household uses of water include typically “indoor” uses such as drinking, cooking, and sanitation as well as “outdoor” uses such as watering gardens and lawns. Household water use is connected to food in the FEW nexus because households use water for food preparation and, in some cases, for growing their own food.

Household water use can also be divided according whether it is self-supplied, from a public supply system, or from private vendors. In the United States, self-supplied water accounts for about 13 percent of household use and is predominantly from groundwater (i.e., private wells). A vast majority comes from public suppliers and very little from vendors; however, in other parts of the world, these percentages are very different.

Although water withdrawn by public supply systems, which is sometimes referred to as municipal use, is primarily distributed for household water use, it can also serve other purposes, such as commercial, public sector, and industrial uses. Therefore, municipal water use and domestic water use are closely related but are not necessarily the same thing.

Like other uses, the value of water for household use can be represented by a marginal benefit or demand curve; however, there are several issues and challenges with measuring this demand.

First, if one wishes to consider the value to households from all sources combined (i.e., self-supplied, public, and private sources), then one cannot ignore the fact that water is essential for human survival and that, below some threshold, economic trade-offs between water and other types of consumption involve very difficult ethical issues. For example, the World Health Organization (2021) estimates that “a minimum of 7.5 litres per capita per day will meet the requirements of most people under most conditions….A higher quantity of about 20 litres per capita per day should be assured to take care of basic hygiene needs and basic food hygiene.” Below these types of thresholds, the concept of private WTP for water is not particularly meaningful for calculating either the marginal or total value of water. Therefore, it is usually more meaningful to assess the marginal benefits of household water use from a particular source (i.e., public water supplier) when alternative sources are available (or, when using a perspective involving all available sources but only considering levels of use that sufficiently exceed minimum survival requirements).

To illustrate how the benefits of publicly supplied water can be conceptualized and measured, Figure 17 shows a simple case with a linear household-level demand curve for water. In situations where households lack or have insufficient access to a public water distribution system, it is assumed that the household can pay a price of p_t,0 for water from alternative sources, such as private vendors (including the economic cost for fetching/buying/storing water). If water is only available at this price, then the demand curve implies that a household would consume w_t,0 per period t. Alternatively, with unlimited access to water from the public water distribution system, if the price per unit of water through the system is p_t,1, then the household’s quantity of water demanded during period t would be w_t,1.

Figure 17.Household benefits of publicly provided water with linear water demand

With this structure, we can estimate the household-level benefits of any actual level of water available from the public system. For example, if water is limited to w_t,2 as shown in Figure 17, then the benefits of this supply are equal to the area A+B+C. The area A represents the avoided expenditures per period t on water from the costlier alternative source (p_{t,0 *} w_t,0). The area B+C represents the household’s WTP for the additional amount from w_t,0 to w_t,2. In short, the total benefits are represented by the area under the demand curve, capped at the price of the alternative source.

It is important to note that the benefits in Figure 17 represent at-site values (i.e., at the point of use by the household). The net benefit of public water supply to the household at the point of use can then be calculated by deducting the variable delivery costs of supplying water to the household. Variable costs refer to those costs, such as pumping costs, that depend directly on the quantity of water supplied. The aggregate net benefits of water supplies can therefore be estimated by summing household-level net benefits across all affected households.

Even with this conceptual framework, a second challenge is in estimating demand curves for household water. They are difficult to measure in practice because prices for household water use are typically not established through market-based supply and demand interactions. Consequently, reliable empirical estimates of water demand typically are somewhat limited. Moreover, in many cases, particularly in less-developed countries, household access to public water supplies is rationed in such a way that the marginal benefit to households is greater than the price they are charged. This situation is shown in Figure 17, where, at the low price p_t,1, the quantity of water demanded is relatively high (at w_t,1), but if the amount of water actually supplied were less (w_t,2), the marginal would be equal to p_t,2.

Third, the demand for water and its value in household use depends on the quality of the water for human consumption and other uses and on the ease of access and reliability of water at its point of delivery. Water quality management and water distribution systems to households are energy- and infrastructure-intensive; thus, supplying reliable and safe drinking water is often constrained by public and private sector capital investments. The role and contribution of these factors must be considered in developing or interpreting value estimates.

Empirical evidence regarding the value of water in household consumption generally comes from two kinds of studies, described below.

Econometric Estimates of Water Demand and Price Elasticity for Household Use

To date, most of the empirical research on household water demand has been conducted in industrialized countries, particularly in the United States, with a focus on estimating the price elasticity of this demand. Many of these studies also examine and estimate income elasticities of demand. Summaries of this literature can be found in meta-analyses conducted by Espey et al. (1997) and Dalhuisen et al. (2003), the latter of which included demand elasticity estimates from 64 studies. Most of these studies find that household water demand is relatively inelastic (with average price elasticity estimates in the -0.4 to 0.5 range). A smaller number of studies have been conducted in low- and middle-income countries, but the results are similar. Nauges and Whittington (2010) identify and summarize estimates from 11 studies, finding price elasticities in the range of -0.3 to -0.6. One of the challenges with applying these price elasticity estimates to calculate benefits (i.e., the area under the curve in Figure 17) is that, as previously mentioned, water prices for households are often set below market clearing prices. As a result, even if the level of water use is observed (w⁰), the height of the demand curve at that point (i.e., the market clearing price, which is greater than P^w), may not be known. Without knowing both coordinates, an elasticity estimate by itself cannot be used to trace out the demand curve.

Other Nonmarket Valuation Approaches Estimating WTP for Water

A main alternative approach for estimating households’ WTP for water from private connections is using stated preference methods. Several survey-based preference elicitation studies, including contingent valuation and choice experiment (conjoint analysis) studies, have been conducted around the world, particularly in developing countries. Summaries of this literature can be found in meta-analyses by Aylward et al. (2010), which analyzed results from 44 contingent valuation studies, and Van Houtven et al. (2017), which included results from 69 stated preference studies.

One of the challenges with applying results from these studies is that the “commodity” being valued is typically access to piped and treated water rather than a specific quantity of water. To translate from access to volume, Aylward et al. (2010) assume access is on average equivalent to 30 liters per person per day (based on a World Health Organization framework). They estimate an average WTP of $0.594 per m³, with a range of $0.008 to $2.88 in 2008 dollars. However, even this approach and estimate does not account for how marginal WTP can vary with respect to level of water use. A related issue is that many stated preference studies focus on WTP for higher-quality and more-reliable tap water services rather than WTP for simply acquiring access to piped water. Defining a volume equivalent of this type of change is more difficult.

Another issue is that these studies typically provide an average household WTP estimate for improved access to drinking water rather than a marginal benefit function or demand curve. One approach is to assume that average and marginal WTP are the same (i.e., a perfectly elastic flat demand curve); however, this runs counter to the findings for the previously described water demand studies (e.g., Nauges & Whittington [2010]), which find relatively low demand elasticities with respect to price.

Industrial Sector Benefits

The industrial sector is perhaps the most difficult sector for incorporating marginal benefits into an integrated valuation framework. This is because of data limitations and the proprietary nature of industrial processes, including the technical relationship between water use and output.

There are direct and indirect approaches to estimating the economic benefits of industrial sector water use. Direct approaches include econometric techniques; studies have estimated the value of water to industrial users by estimating the derived demand for water in France (Reynaud, 2003) or by estimating industry cost functions in Canada (Renzetti & Dupont, 2003). Few studies use these approaches, and those that do are mainly restricted to relatively high-income regions because of the data requirements. Demand elasticities or marginal value estimates can be incorporated into hydro-economic optimization models to represent marginal benefits to industrial sector users, though one would need to disaggregate industry-wide demand/benefit curves to industrial users within specific model regions.

An indirect approach would involve deriving value metrics from existing economic data. For example, it is often possible to use social accounting matrices or other macroeconomic datasets to infer the relative contribution of water to a given sector’s value of production, but this approach yields an average value, which is often undesirable as a metric. However, in certain situations, this might be sufficient if industry’s proportion of total water consumption is small relative to other sectors.

Without sufficient data for developing reasonable marginal benefit and cost assumptions for industrial users, there are reasonable alternatives for representing industrial sector water demands within an economic modeling framework. One option is to impose exogenous water allocation requirements that line up with observed allocations. This is useful because it imposes a realistic constraint on the system reflecting current use patterns. In an optimization model, if this is a binding constraint, then the shadow price revealed represents the additional value that could be obtained by relaxing the industrial sector allocation constraint by one additional unit.

Indirect Use and Indirect Nonuse Benefits

As discussed previously and shown in Figure 3, water also provides indirect value to humans by supporting the ecosystems and natural processes that they directly value. For example, freshwater flows into an estuary can be an essential natural input for fish habitat and for marshland ecosystems that support waterfowl. In these cases, humans may directly value the fish as a source of food and the waterfowl as a game species for hunting (or they may receive nonuse values from these species). They may not understand or perceive the role that water plays in providing these wildlife resources, but they nonetheless receive benefits from the role.

To conceptualize and estimate these indirect benefits from water, it is helpful to think of water as an input to an ecological production function (EPF) (Bruins et al., 2017). An EPF is a natural process that generates outputs, which may be directly valued by humans. For example, in the previous example, estuarine habitat processes are an EPF that requires freshwater inputs to support the natural production of fish stocks.

In these cases, estimating the value of water is a two-stage process. First, one must estimate the EPF relationship between the quantity of water entering or present in the system and the quantity of the component of nature that humans directly value (e.g., fish abundance). This estimation may, for example, involve conducting or using the results from environmental/ecological flow analysis.

Second, one must estimate the marginal benefit (demand) curve for the EPF output. The process and methods for estimating these natural outputs are fundamentally the same as for water. From a conceptual standpoint, the values can be organized and categorized with a TEV framework like the one in Figure 3. In other words, the framework can distinguish between consumptive and nonconsumptive use values and nonuse values for the output. It can also distinguish between commercial/market-based direct uses of the output (e.g., commercial fishing) and household uses (e.g., recreation). Including nonuse values is particularly challenging, especially for lower-income regions, because it requires new or existing applications of survey-based stated preference approaches, which can be relatively expensive to implement.

Operationally, a hydro-economic model can reflect these marginal benefits by directly valuing water storage or instream flows. This approach allows nonmarket-use or nonuse allocations of water to compete directly with other use allocations (agriculture, energy, household consumption). Alternatively, minimum flow or storage thresholds can be established to ensure adequate water availability for ecosystem function (Do et al., 2020; McCarl et al., 1999).

Optimization of Water Allocation Across and Within Sectors

The last major component of the hydro-economic modeling framework is an economic optimization module, which pulls together elements from the previously described water use (and nonuse) benefit components. Optimization in this context typically refers to selecting an allocation of resources (water and land) and input use (energy and other inputs to economic production systems) that maximizes the total benefits across users and nonusers subject to defined physical, economic, or other relevant constraints.

The objective function can be broadly defined and expressed as in Equation 12. The function uses either the marginal benefits (MB) or total benefits (TB) of water in each sector (s = 1…S) and across different “nodes” (n = 1…N) or spatial units that define the geographic boundaries of the water resource management system. Note that this function represents just a one-year optimization model. In this example, total benefits and costs are maximized for a given year, resulting in a perfect foresight optimization framework for a given year. Monthly time steps typically define hydro-economic models, although hydrologic and energy dispatch frameworks often operate at more-frequent time steps. To reflect an intertemporal model over many years, one would need to add an annual time step and an appropriate discount rate.

$$\begin{align} {Max}\ {Total}\ {Benefits} &= \sum_{n}{\sum_{s}{\int_{0}^{W_{s}}{{MB}_{s}(W_{s})}}} \\ &= \sum_{n}{\sum_{s}{{TB}_{s}(Q_{s})}} \end{align} \tag{12}$$

For each sector, the marginal benefits will follow a particular functional form (Equation 13). For agricultural benefits, this could be a general set of profit functions conveying the net returns to crops with different levels of irrigation inputs or a continuous marginal benefit function, as described above. For energy sector benefits, f_s() could be as simple as a constant net return per unit of energy generated (energy price less variable costs per unit).

$$MB_{s}\left( W_{s} \right) = f_{s}(W_{s}) \tag{13}$$

The hydro-economic model will represent the hydrologic system in an aggregated fashion, but in general will represent hydrologic continuity over space and time. For surface water systems, this continuity can be represented by Equation 14:

$$\begin{align} \sum_{k}{Storage_{nkt}} = &\sum_{k}{Storage_{nk,t - 1}} - \sum_{s}D_{{nst}} - W_{n \rightarrow n + 1,t} \\ &+ {Inflo}w_{{nt}} + \sum_{s}{\phi_{{ns}}D}_{{nst}}{+ W}_{n - 1 \rightarrow n,t} \end{align}\tag{14}$$

In this equation, variables are defined as follows:

• n denotes node, k denotes storage unit (reservoir), s denotes sector, and t denotes time period.

• ${Storage}_{nkt}$ is the stock of water stored at the end of period t in each reservoir k in node n. Storage variables can also be used to reflect groundwater dynamics in systems where both surface and groundwater supplies are accessed.

• $W_{n \rightarrow n + 1,t}$ is the flow of water from node n to downstream node n+1 during period t.

• $D_{nst}$ is the flow of water diverted to sector s from node n during period t.

• ${\phi}_{ns}$ is the return flow portion of water diverted to sector s from node n.

• ${Inflow}_{nt}$ is the other inflow (e.g., from direct rainfall or surface runoff) to node n during period t.

In other words, as also represented in Figure 18, total water stored (e.g., in millions of m³) in a node at the end of a time period (e.g., month) is equal to the total water stored at the beginning of the period, plus all inflows and minus all outflows during the period (in millions of m³ per month). Although this framework does not explicitly include groundwater stocks or flows, it can be expanded and adapted to include groundwater storage units (aquifers) and flows to (recharge) and from (withdrawals and discharges to surface water) these units.

Figure 18.Representation of the water balance and continuity constraint during a single time period

Note: Because the figure represents a single time period, the t subscript is suppressed in the figure.

To represent water resource constraints, one can implement upper bounds (capacity limits) on both storage levels and surface water flows. Conversely, we can adapt the model to represent policy-based minimum instream flow requirements by imposing a lower bound on total flow between nodes or to impose constraints that maintain ecosystem function. Furthermore, to calibrate to existing water allocations or institutional arrangements, constraints can represent upper or lower bounds on total withdrawals for different user groups (e.g., a minimum required level of withdrawals for domestic consumption), though such constraints can limit a model’s ability to consider allocation schemes that improve on status quo allocation.

Other constraint sets commonly built into hydro-economic modeling routines represent economic or physical limits on water allocation. For example, models often reflect physical limits on water withdrawal and distribution consistent with capacity of existing infrastructure (e.g., pumps, water treatment, and distribution systems), but include options for expanding capacity at an additional cost. Other physical constraints include minimum or maximum storage levels in reservoirs, flood control requirements, or minimum streamflow requirements to represent important thresholds for ecosystem function.

Other constraint sets often reflect variation in economic inputs and parameter assumptions. For example, household demand for water, energy, and recreational opportunities at storage reservoirs likely vary seasonally. Furthermore, producer prices for agricultural and industrial outputs that are water-intensive can also vary temporally. Not accounting for this seasonality in marginal benefits or resource demands can bias spatial and temporal allocation results from a hydro-economic framework. Each subcomponent of the FEW nexus (e.g., food production systems) may require additional constraints to reflect context-specific realities. Hydro-economic models vary setting-to-setting in this regard, but food, energy, and water systems are linked via ecological and economic production functions. Recent examples of hydro-economic models that capture FEW system components with detailed documentation of structural equations and data include Bekchanov et al. (2019), Jeuland et al. (2014), and Do et al. (2020).

Conclusions

Hydro-economic models are particularly well-suited for FEW nexus analyses because, by design, they integrate representations of water resource systems (i.e., hydrologic models) with those of human behavioral systems (e.g., economic models of food and energy production). Much of this report has described how food, energy, and water systems are independently captured within a hydro-economic framework; the advantage of this methodology is that sectoral interactions are explicitly captured through resource competition, supply-side considerations, and marginal benefit functions. In addition to capturing these inextricable FEW system linkages, hydro-economic modeling enables scenario analysis, multiobjective optimization, and goal programming to analyze implications of scenario assumptions on competing FEW nexus objectives and sustainable development goals.

Hydro-economic models thus explicitly account for trade-offs and synergies in water use between food, energy, and water management systems. To explain the approach, we describe how watershed or groundwater management schematics can be built to represent a water management system, how economic costs and benefits can be parameterized for different sectors to reflect marginal benefits of alternative consumption activities, and how these water supply and demand systems can be connected through an integrated modeling and optimization approach. The goal is to offer a generalizable, flexible, and geographically portable modeling approach for optimizing the allocation of scarce water resources across multiple users, including food and energy producers.

Although detailed in many respects, the framework is general enough to accommodate a variety of hydrologic and economic systems and models. We offer examples from the literature and our own experience to illustrate the approach. The basic framework can be expanded in several ways, however, to address more-complex systems and issues. First, the hydrologic model component can be expanded to address interactions and feedbacks between surface water and groundwater systems. To date, most hydro-economic applications have treated these separately or offered only a coarse representation of groundwater dynamics and surface-groundwater interactions. Second, the complexity of the models can be increased by simultaneously analyzing trade-offs across multiple dimensions of water use, including spatial, sectoral, and temporal dimensions. Even within sectors, there can be multiple dimensions. For example, in agriculture, water allocations can depend on choice of crop mix, number of acres to irrigate, and irrigation intensity (i.e., annual inches per acre).

Third, analyses of economic trade-offs in water use across the FEW nexus can be expanded to address uncertainties regarding both the supply and demand for water. For example, on the supply side, there are key uncertainties regarding how changes in climate and land use will affect instream flows, and on the demand side, there are uncertainties about population and economic growth. These supply and demand uncertainties can be incorporated using stochastic analysis and optimization (see, for example, Tilmant et al. [2020]).

Finally, hydro-economic models have not been widely used to address the many ways water quality affects the FEW nexus. For example, poor water quality such as high salinity in irrigation water can reduce agricultural productivity. Pollutants in households’ cooking water can contaminate the food they consume. Thermal water pollution can negatively affect cooling water efficiency for energy generation. At the same time, agriculture and energy production can often have negative impacts on water quality, and energy is a key input for treating water pollution. However, in most hydro-economic models, water is treated like a homogeneous good of a given quality, even though this is clearly not the case in some settings. For example, in Guatemala, 98 percent of the untreated water in the country contains E. coli (Braghetta, 2006); access to treated piped water is low (Kuper et al., 2018); and diarrhea, likely caused by drinking water contamination, is the number two cause of child mortality (MSPAS, 2018).

The basic hydro-economic framework described in this document could also be adapted and expanded to incorporate water quality changes and effects. For example, water quality changes could be addressed in ways that are equivalent to increasing water scarcity, such as using salinity, temperature, or pollutant thresholds to in effect exclude some water from the useable resource base. Similarly, the effects of agriculture and energy production on water quality can be explicitly incorporated into the water system modeling component. Future research that integrates the modeling of water resources with water quality, and more broadly, FEW sustainability and quality, will provide critical advancements in the ability to plan for and respond to natural resource needs and limits.

Given these options for expanding the modeling framework, selecting the appropriate types and level of detail in modeling components will ultimately depend on the needs and data availability of specific applications. It is important to emphasize that the success of building and applying hydro-economic models will often depend on data and input from local stakeholders.

It is also important to recognize the limits of hydro-economic models for analyzing FEW nexus issues. First, although these models are well-suited for analyzing costs and benefits within defined sectors, they are not as suitable on their own for analyzing economy-wide or multisectoral general equilibrium impacts. For example, if water scarcity at a regional or national level limits or increases the costs of energy production, the resulting increase in energy prices can have ripple effects in other parts of the economy by, for instance, increasing the cost of food production and food manufacturing. These higher costs can then change the demand for and use of water by the affected sectors. To analyze these broader connections, feedbacks, and trade-offs between the energy, agricultural, water, and other sectors requires methods for pairing hydro-economic models with economy-wide models such as input-output and computable general equilibrium models (Bekchanov et al., 2017).

Second, hydro-economic models are not necessarily well-matched for evaluating specific technological approaches at the FEW nexus, such as recycling of oilfield water or using renewable energy to power water desalination for cropland irrigation. Analyzing the cost-effectiveness and environmental impacts of these potential technological solutions to water scarcity generally requires more in-depth facility-level analyses.

Despite these limitations, hydro-economic models offer a theoretically grounded and versatile framework for analyzing trade-offs and connections within the FEW nexus. In particular, hydro-economic modeling offers the ability to run simulations or explore tradeoffs of different resource management strategies under scenarios of socioeconomic, policy, and climate change.

Acknowledgments

The authors acknowledge internal research and development support from RTI International for this effort, including the RTI Grand Challenge project Building Resilience in Food, Energy, and Water Systems.